Coleperiódico
viernes, 5 de junio de 2015
miércoles, 20 de mayo de 2015
Noticias sobre matemáticas
Daniel Tammet, escritor y prodigio de las matemáticas
Hace diez años, Daniel Tammet (Londres, 1979) –ahora escritor afincado en
París (Francia)– se enfrentó a uno de los retos más difíciles de su vida:
recitar 22.000 decimales del número Pi. Lo logró en poco más de cinco horas,
sin fallos. En su nuevo libro La poesía de los números describe cómo consiguió
transformar una serie infinita de números en una experiencia poética en la que
se mezclan números y letras, colores y formas, amor y belleza.
“Yo no soy matemático”, dice Daniel Tammet en perfecto francés. Repite en
varias ocasiones esta afirmación durante la conversación telefónica por una
sencilla razón: las matemáticas no son más que el ejercicio de su imaginación.
Para este escritor, procedente de una familia de nueve hermanos, los números
representan todo su mundo.
Y le hablan tanto como lo hacen las letras. De niño se identificaba con el 4
porque esa cifra para él significa tímido. “Me gustaba porque yo era así”,
confiesa Tammet, que también padece trastorno del espectro autista, aunque
ahora “es muy poco visible”. En la actualidad, el escritor prefiere el 11, un
número que le recuerda a su pareja, y que es sinónimo de belleza y cariño.
“Tengo una relación casi de amistad con todos estos números con los que
comparto mi vida desde mi más tierna infancia”, apunta el autor. Aunque le
suscitan las mismas emociones, sus amigos ‘los números’ en la actualidad ya no
ocupan el mismo lugar. Ahora, Tammet vive en París, tiene una carrera como
escritor, pareja y amigos, por lo que “ya no desempeñan el mismo papel”. Pero
para él, las matemáticas son esenciales para entender cuestiones relativas a
nuestra sociedad y al tiempo.
El libro La poesía de los números. Cómo las matemáticas iluminan mi vida
–de la editorial Blackie Books– recoge una mezcla de referencias personales,
sociales y filosóficas sin dejar de hablar de matemáticas. Pero no está escrito
por un matemático o un científico. Tammet ha tenido un recorrido más literario:
“Los que han seguido este mismo camino tienen miedo de hablar de matemáticas, y
es una pena porque las matemáticas están por todas partes, son universales y
son una parte integral de nuestra existencia”.
Como ya pensaban Tolstói y Shakespeare, fascinados por el poder y la magia
que desprenden los números, el escritor británico considera que las matemáticas
no se limitan a un ámbito puramente científico y abstracto, sino que también
llegan a los artistas y escritores. En definitiva, a cualquiera que sea
curioso.
Sin embargo, para Tammet no ha sido fácil. Debido a su trastorno, de niño
hablaba muy poco y cuando lo hacía, le costaba expresarse. “No era como los
demás”, declara. El inglés era su idioma materno, pero a la vez no lo
consideraba como el primero. “No tenía el sentimiento de pertenecer a esa
lengua”. Hoy utiliza el francés como su idioma cotidiano.
Su contacto con las palabras ha sido aún más arduo. “Eran como un puzle que
quería descifrar y descodificar para entenderlas”. Pero a esto se añadió el
fenómeno de la sinestesia: Tammet ve las palabras y los números con colores,
formas y texturas. “Esto me ayuda a aprender mejor”. Como cada palabra se
expresa y tiene un sonido diferente en cada idioma, un mismo término puede
tener colores distintos.
Pongamos un ejemplo: la palabra ‘árbol', que en francés es ‘arbre’, es de
color rojo –porque el sonido empieza por ‘a’–, pero en inglés ‘tree’ es de
color naranja para el autor. En función del idioma, las palabras adoptan un
color. “Siempre intento encontrar una relación y un sentido a las palabras.
Cada idioma es como un poema o un cuento”, afirma Tammet quien habla cuatro
idiomas de manera fluida y se defiende en otros seis, incluidos el esperanto.
“Al nacer, creo que cada cerebro funciona como el mío para aprender la
primera lengua. Más tarde estas capacidades se pierden al imponer una educación
y una cultura”, subraya el autor, quien revela que el autismo le ha protegido
de alguna manera.
A pesar de ser su tercer libro –el primero se publicó hace 10 años– y de la
“evidente” evolución de su vida en estos años, Tammet señala que sigue habiendo
muchos prejuicios respecto a las personas con trastorno del espectro autista.
“La gente piensa que no somos capaces de ser creativas y de tener buena
memoria, ni siquiera de ser escritores o artistas”.
Su libro desmiente todos estos clichés. Muestra otro aspecto de sí mismo,
de alguien que lee mucho y que viaja. “Ha sido una manera de recoger
curiosidades respecto a nuestro mundo, y de mostrar en qué se diferencia de lo
que yo veo”, indica el autor quien en el fondo se considera muy normal. “Me
interesan los otros y el mundo exterior”.
Pero, en parte, se equivoca. Daniel posee una mente prodigiosa. Prueba de
ello fue la experiencia de recitar 22.000 decimales del número Pi (3,14159...).
Lo hizo en cinco horas y nueve minutos; y su estrategia fue considerar al
número Pi como un poema universal en el que se refleja lo que siente por los
números.
En su libro enfoca esta vivencia desde un punto de vista más literario:
“Recitar los decimales de Pi no es contar números, sino narrar una historia”,
comenta el autor, que en unas pocas horas encarnó el infinito que representa el
número Pi.
“Aunque escribamos todos los decimales de Pi sobre un papel, nunca habrá
suficiente espacio para todos. Es un número que sobrepasa todo nuestro entendimiento
y las fronteras de nuestro universo”, añade el escritor, que logró memorizar
los decimales a través de la emoción.
El secreto es que Tammet ve belleza en los números. No solo eso, también
visualiza colores, formas, texturas, emociones y personalidades, y los
convierte en una historia y les encuentra sentido. “No se trata de memorizar y
aprender técnicas para recordar ‘tontamente’ estas combinaciones. Es una
búsqueda hacia la comprensión y el sentido subjetivo”.
El autismo ha tenido algún efecto en el desarrollo de su cerebro. “Ha
podido facilitarme unas conexiones neuronales y complicarme otras, pero a esto
hay que añadir que de niño leía mucho. Encontraba en los libros un refugio
cuando el mundo me parecía demasiado complejo o grande”, recuerda. Esto
alimentó su imaginación y su curiosidad, pero también lo hicieron el amor por
las cifras, las palabras y sus seres queridos.
La gente a veces se confunde y piensa que es frío y racional, como si fuera
matemático. Pero “para nada es así”, zanja. A Daniel le mueven las emociones.
De pequeño le costaba comunicar los sentimientos, pero hoy ya lo ha superado.
Con su tercer libro, Tammet demuestra que no es necesario elegir entre el
universo de los números y el de las letras porque ambos “nos pertenecen a
todos”.
Fuente: SINC/Marcos, A.(15 de mayo de 2015).Daniel Tammet, escritor y
prodigio de las matemáticas.Noticias de la ciencia.
Recuperado de . http://noticiasdelaciencia.com
Matemáticas contra el cáncer
Cuando
las matemáticas se emplean para ayudar a comprender el comportamiento y
resolver los problemas prácticos de la vida real, hablamos de “matemática
aplicada”. Campos tan distantes y tan diversos como la física, la economía, la
biología, la arquitectura o los juegos son tan solo unos pocos ejemplos de la
multitud de ramas del conocimiento que deben a las matemáticas tanto la resolución
de los problemas más simples como sus avances más espectaculares. Hoy les
ofrecemos una visión sorprendente de uno de esos muchos campos de aplicación:
la oncología matemática.
Resulta difícil de entender qué relación puede
existir entre las matemáticas y el cáncer. Un tumor se origina cuando una
célula de un organismo se niega a morir y se divide sin control dando lugar a
generaciones de células hijas que proliferan hasta tal punto de poner en
peligro la existencia del organismo completo. Con esta descripción es fácil
entender que cada tipo de célula de nuestro cuerpo, si por alguna razón se
vuelve cancerosa, puede generar un tumor. Dado que tenemos más de un centenar
de tipos distintos de células en nuestro organismo, pueden surgir cientos de
tipos de tumoresdiferentes. Comprender cada uno de ellos, detectarlos a tiempo,
conocer su evolución futura, encontrar sus debilidades para aplicar
tratamientos adecuados, es un reto para la medicina y para la ciencia en
general.
Un
conjunto tan diverso y peligroso de enfermedades no puede ser vencido con un
remedio simple. Los oncólogos necesitan la ayuda de los biólogos, de los
físicos, de los químicos, de los informáticos, de los ingenieros y de los
matemáticos, como nos explica nuestro invitado de hoy en Hablando con
Científicos: Juan Belmonte Beitia es investigador del Grupo de Oncología Matemática que desarrolla su labor en el Instituto de Matemática
Aplicada a la Ciencia y la Ingeniería de la Universidad Castilla-La Mancha.
Estudiar todos los factores que intervienen en un
sistema biológico cualquiera es prácticamente imposible. La cantidad de
variables que intervienen, desde las que controlan las reacciones químicas
entre átomos y moléculas hasta las que intervienen en la interacción,
crecimiento y evolución de organismos completos es inmensa. Sistemas biológicos
hay muchísimos, una población de bacterias que crece, la proliferación de un
enfermedad infecciosa, los latidos de un corazón como producto de la acción
coordinada de miles de millones de células o, como en el caso que nos ocupa, la
proliferación de células cancerosas en un tumor, son unos pocos ejemplos. El
modelo matemático no tiene en cuenta a todas las variables, tan sólo incluye
unas pocas en un conjunto de ecuaciones, pero con ellas es posible extraer,
teóricamente por supuesto, ciertos comportamientos del sistema completo y su
evolución con el tiempo. Después, si el modelo es lo suficientemente bueno, sus
resultados se acercarán al comportamiento real y ello permitirá obtener
respuestas sobre el comportamiento futuro del sistema.
Un tumor es sistema biológico formado por una
masa de células que crece y que se extiende por el organismo, así pues,
utilizando como variables ciertos parámetros de éste, se puede obtener un
modelo matemático que intente imitar su evolución futura. Para elaborar un
modelo fiable se debe partir de datos reales, facilitados por hospitales, centros
de investigación y pacientes. Con los datos facilitados mediante imágenes de
resonancia magnética nuclear y otras técnicas de imagen y análisis tomadas a
pacientes reales, los investigadores del Grupo de Oncología Matemática calculan
factores de crecimiento de los tumores y elaboran modelos matemáticos que
simulan el comportamiento de varios tipos de cáncer cerebral. Una vez
desarrollados los modelos, con la utilización de potentes ordenadores, se
pueden obtener soluciones numéricas que permiten calcular la evolución futura
del tumor.
Lógicamente, las soluciones facilitadas por el
modelo matemático por sí solas no son suficientes, como hemos dicho, los
sistemas biológicos son muy complejos, pero estos modelos permiten simular
distintas situaciones cuando las condiciones cambian y establecer su evolución
teórica en función del tamaño inicial del tumor, su capacidad de difusión o la
administración de terapias concretas. Estos datos, junto a los obtenidos por
otros medios, pueden ayudar al oncólogo a escoger el tratamiento más adecuado
para cada paciente.
Fuente: (19 de septiembre de 2014).Matemáticas contra el cáncer. Noticias
de la ciencia.
Recuperado de http://noticiasdelaciencia.com
Las matemáticas
amplían el conocimiento sobre el cerebro
La combinación de las versiones más modernas de análisis
matemático, registros eléctricos y biofísica ha permitido al Consejo Superior
de Investigaciones Científicas (CSIC) de España diseñar una técnica capaz de
visualizar la actividad de varios núcleos cerebrales a través del registro de
uno de ellos interconectado a todos los demás. El hallazgo, que ha sido
publicado en la revista The Journal of Neuroscience, permite realizar estas observaciones
de forma simultánea y en tiempo real.
La nueva técnica desarrollada por el equipo del CSIC permite la lectura de la actividad eléctrica simultánea de varias zonas del interior del cerebro en cada una de las cuales se percibe a su vez la de otros tantos núcleos cerebrales conectados entre sí. El análisis matemático de componentes independientes, optimizado en este caso para registros intracerebrales, permite separar cada uno de estos flujos para interpretarlos de forma independiente.
El investigador del Instituto Cajal del CSIC Óscar Herreras, que ha dirigido el trabajo, compara este proceso con la grabación a través de varios micrófonos de una habitación en la que varias personas hablan simultáneamente: “Las voces serían procesadas por esta técnica matemática que devuelve el sonido de cada persona por separado de forma que su mensaje es perfectamente comprensible”.
Los resultados preliminares indican que la información entre núcleos del sistema nervioso fluye a través de ciertas cadenas preferentes de neuronas. A través de ellas, en cada instante, un grupo distinto de neuronas de cada núcleo emite un mensaje hacia otros núcleos conectados. Este continuo cambio entre los grupos de neuronas que emiten señales es el que va codificando los mensajes emitidos por el sistema nervioso.
Dado que los núcleos cerebrales están casi siempre activos, es difícil conocer su implicación en distintas funciones. Por ello, Herreras, considera “imprescindible registrar la actividad del sistema nervioso en su totalidad”.
Según Herreras, “la complejidad del funcionamiento del sistema nervioso impide que pueda ser estudiado en profundidad de forma íntegra con las técnicas actuales”. Aunque la resonancia magnética sí ofrece una imagen del cerebro completo, Herreras considera que son imágenes “muy borrosas, de mala calidad y que apenas captan una pequeña fracción de lo que realmente ocurre”.
Herreras asegura que “la velocidad de esta técnica permite obtener por primera vez en tiempo real la lectura de grandes flujos de información y averiguar qué núcleos participan en su procesamiento y en la ejecución de tareas”. El equipo ya ha iniciado una serie de experimentos con animales despiertos que permitirán “leer la actividad neuronal y asociarla a comportamientos concretos”, añade Herreras.
El investigador el CSIC concluye: “Esta aproximación ayudará, también, a detectar patrones alterados en el flujo de información en patologías neurológicas, lo que podría contribuir a identificar las regiones del cerebro donde se origina la alteración y las posibles dianas terapéuticas”.
La investigación ha contado con la colaboración de un investigador del Departamento de Matemáticas Aplicadas de la Universidad Complutense de Madrid Valeri Makarov.
Fuente: CSIC. (27 de agosto de 2012). Las matemáticas amplían el conocimiento sobre el cerebro. Noticias de la ciencia.
La nueva técnica desarrollada por el equipo del CSIC permite la lectura de la actividad eléctrica simultánea de varias zonas del interior del cerebro en cada una de las cuales se percibe a su vez la de otros tantos núcleos cerebrales conectados entre sí. El análisis matemático de componentes independientes, optimizado en este caso para registros intracerebrales, permite separar cada uno de estos flujos para interpretarlos de forma independiente.
El investigador del Instituto Cajal del CSIC Óscar Herreras, que ha dirigido el trabajo, compara este proceso con la grabación a través de varios micrófonos de una habitación en la que varias personas hablan simultáneamente: “Las voces serían procesadas por esta técnica matemática que devuelve el sonido de cada persona por separado de forma que su mensaje es perfectamente comprensible”.
Los resultados preliminares indican que la información entre núcleos del sistema nervioso fluye a través de ciertas cadenas preferentes de neuronas. A través de ellas, en cada instante, un grupo distinto de neuronas de cada núcleo emite un mensaje hacia otros núcleos conectados. Este continuo cambio entre los grupos de neuronas que emiten señales es el que va codificando los mensajes emitidos por el sistema nervioso.
Dado que los núcleos cerebrales están casi siempre activos, es difícil conocer su implicación en distintas funciones. Por ello, Herreras, considera “imprescindible registrar la actividad del sistema nervioso en su totalidad”.
Según Herreras, “la complejidad del funcionamiento del sistema nervioso impide que pueda ser estudiado en profundidad de forma íntegra con las técnicas actuales”. Aunque la resonancia magnética sí ofrece una imagen del cerebro completo, Herreras considera que son imágenes “muy borrosas, de mala calidad y que apenas captan una pequeña fracción de lo que realmente ocurre”.
Herreras asegura que “la velocidad de esta técnica permite obtener por primera vez en tiempo real la lectura de grandes flujos de información y averiguar qué núcleos participan en su procesamiento y en la ejecución de tareas”. El equipo ya ha iniciado una serie de experimentos con animales despiertos que permitirán “leer la actividad neuronal y asociarla a comportamientos concretos”, añade Herreras.
El investigador el CSIC concluye: “Esta aproximación ayudará, también, a detectar patrones alterados en el flujo de información en patologías neurológicas, lo que podría contribuir a identificar las regiones del cerebro donde se origina la alteración y las posibles dianas terapéuticas”.
La investigación ha contado con la colaboración de un investigador del Departamento de Matemáticas Aplicadas de la Universidad Complutense de Madrid Valeri Makarov.
Fuente: CSIC. (27 de agosto de 2012). Las matemáticas amplían el conocimiento sobre el cerebro. Noticias de la ciencia.
Recuperado de http://noticiasdelaciencia.com
Una escala matemática predice el riesgo de muerte por insuficiencia cardiaca
Una escala matemática para
predecir el riesgo de mortalidad de los pacientes con insuficiencia cardiaca
durante el primer año tras el diagnóstico permite planificar de una forma más
individualizada su tratamiento y así conseguir modificar la evolución de la
enfermedad y mejorar su pronóstico.
La escala es el fruto de un proyecto de investigación financiado por el Fondo
de Investigación Sanitaria del Instituto de Salud Carlos III y realizado por la
Unidad de Investigación Clínica del Instituto de Investigación del Hospital 12
de Octubre i+12, en colaboración con los hospitales Virgen del Rocío y Valme de
Sevilla, todos ellos en España.
Para realizar el estudio se ha llevado a cabo un seguimiento durante un año de
600 pacientes con insuficiencia cardiaca recién diagnosticada, evaluando el
tipo de patología cardiaca, las concentraciones de sodio y creatinina, y la
capacidad de autonomía del paciente.
Esta última variable supone una novedad importante en este tipo de
investigaciones, ya que la tendencia en los trabajos de investigación sobre
riesgo en insuficiencia cardiaca es buscar marcadores biológicos complejos o
alejados de la práctica clínica cotidiana que se identifiquen con factores
pronóstico de la enfermedad, sin observar y cuantificar por ejemplo variables
simples como el grado de autonomía para las actividades diarias de la persona a
valorar.
Con estos datos, se ha elaborado la escala o regla de predicción clínica que
permite determinar el riesgo de mortalidad de un paciente durante el primer
año, tras iniciarse la enfermedad.
Según la información objeto de estudio en esta investigación, aproximadamente
el 30% de los pacientes ha fallecido antes de cumplirse el primer año desde el
diagnóstico inicial de la insuficiencia cardiaca.
Este proyecto forma parte de la aportación del grupo español a la iniciativa
conocida como Energing Risk Factors Collaboration, iniciada en 2006 por una
agrupación internacional de científicos que pretende profundizar a través de un
macroestudio en el conocimiento de nuevos factores de riesgo cardiovascular y
en el comportamiento de los ya conocidos.
Tras repasar el papel de los lípidos, la glucemia y los marcadores
inflamatorios en una cohorte de más de un millón de individuos, ha podido
especificarse con mucha mayor precisión el tipo de relación que existe entre
algunos componentes metabólicos y el riesgo de sufrir una enfermedad
cardiovascular.
Estas investigaciones, divulgadas en la revista Cardiology Journals, forman
parte de una serie de artículos recogidos en publicaciones científicas como The
Lancet, Jama y New England Journal of Medicine.
Esta patología se produce
cuando el corazón no es capaz de bombear sangre en la cantidad requerida por el
cuerpo humano para desarrollar sus actividades habituales. Se estima que la
insuficiencia cardiaca afecta al 6,8 por ciento de los españoles mayores de 45
años, llegando a ascender hasta el 15 y 20% en las personas mayores de 85 años.
Fuente: SINC. (27 de agosto de 2013). Una escala matemática
predice el riesgo de muerte por insuficiencia cardiaca. . Noticias de la ciencia.
Recuperado de http://noticiasdelaciencia.com
La habilidad con las matemáticas tiene un componente innato
Aceptamos que algunas personas nacen con talento para la música, el arte o los deportes. Pero, ¿y para las matemáticas? ¿Algunos individuos simplemente nacen con mejores habilidades para las matemáticas que otros?
Pues parece que así es, al menos según los resultados de un nuevo estudio
realizado por un equipo de psicólogos de la Universidad Johns Hopkins, en
Estados Unidos.
El equipo de Melissa Libertus, Lisa Feigenson y Justin Halberda, estudió a 200
niños de cuatro años de edad que realizaron varias tareas. El equipo de
investigación midió en ellos la percepción numérica, las habilidades
matemáticas y la habilidad verbal. A los niños se les premió por su
participación con pequeños obsequios, como pegatinas y lápices.
En la tarea de percepción numérica, los investigadores pidieron a los niños que
observaran grupos de puntos azules y amarillos que aparecían en la pantalla de
un ordenador, y que estimaran qué grupo era más numeroso. No era posible
contarlos porque los conjuntos de puntos se mostraban durante muy poco tiempo y
la habilidad para contar de la mayoría de los niños aún no era grande.
Los niños, después de ver fugazmente los conjuntos de puntos, indicaban
verbalmente al investigador cuál de los grupos era el que ellos creían que
contenía más puntos, y entonces el investigador pulsaba el botón
correspondiente.
Algunas comparaciones eran fáciles, como la de entre un grupo de 5 puntos
amarillos y otro de 10 azules. Otras eran bastante más difíciles, como la de
entre un grupo de 5 puntos amarillos y otro de 6 azules.Los niños sabían si habían acertado o no, mediante un pitido de tono alto o bajo.
Usted puede someterse a un test online similar al aplicado a los niños, aquí:
http://www.panamath.org/testyourself.php
A los niños también se les sometió a una prueba estandarizada para medir habilidades matemáticas muy básicas.
Se constató que la precisión de las estimaciones de los niños se correlacionaba con sus habilidades matemáticas.
Según los investigadores, esto significa que el nivel de la capacidad innata de estimación numérica está asociado al grado de eficiencia alcanzado en las matemáticas escolares.
Fuente: SINC. (16 de septiembre de 2011). La habilidad con las matemáticas tiene un componente innato. Noticias de la ciencia.
Recuperado de http://noticiasdelaciencia.com
Introducción a la medida y su relación con la Geometría en Educación Primaria
1- Medidas de longitud
Corresponden a unidades de medida que sirven para saber cuán largo es un objeto. La unidad que se utiliza internacionalmente para medir longitudes, es el metro (m). De esta unidad provienen otras más pequeñas (llamadas submúltiplos) o más grandes (llamadas múltipos).

Cuando se quiere transformar una unidad de longitud que va desde el metro al decímetro o al centímetro se debe multiplicar por 10 o por 100, respectivamente. También se pueden convertir los decímetros a centímetros. Para hacerlo debemos multiplicar por 10 el número de decímetros.
Si se quiere transformar al revés, es decir, desde centímetro a decímetro o a metro, se debe dividir el total de centímetros por 10 y por 100, respectivamente. También se pueden convertir los decímetros a metros, dividiendo por 10 el número de decímetros.
2- Medidas de superficie
Sirven para medir superficies cuadradas, es decir, en dos dimensiones: largo y ancho. La unidad de medida es el metro cuadrado (m2).
Otras unidades mayores y menores son:

La unidad principal de volumen es el metro cúbico.
Otras unidades de volúmenes son:

La longitud y el perímetro
El perímetro es la suma de las longitudes de todos los lados de un polígono. Para descubrir el perímetro de todas las formas geométricas dejo este vídeo que me ha parecido bastante interesante: Cálculo de PerímetroPara la circunferencia el cálculo del perímetro es un poco distinto al mostrado anteriormente pero igual de fácil. Éste se calcula multiplicando 2 por π y por el radio (recuerda que también lo puedes calcular con el diámetro ya que diámetro= 2radio ).
Os dejo unos ejercicios para practicar con los perímetros:
Cálculo de áreas
El área de una figura plana es la medida de su superficie.
Las medidas de superficie en el Sistema Métrico Decimal (SMD) son: metro cuadrado (m2.) y todos sus múltiplos (dam2 hm2 km2 ) y submúltiplos (dm2 cm2 mm2 ).
Áreas:
Os dejo unos ejercicios sobre áreas a ver cómo se os dan ...
Cálculo de volúmenes
El volumen como magnitud es entendido como el espacio que ocupa un cuerpo. La misma posee tres dimensiones, alto, ancho y largo.
Según el Sistema Internacional de Unidades, el volumen es representado por el metro cúbico.
Volúmenes
Teorema de Thales
Si dos rectas cualesquieras se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra.


Ejemplos
1 Las rectas a, b y c son paralelas. Halla la longitud de x.


2 Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas a y b?

Sí, porque se cumple el teorema de Thales.

Teorema de Thales en un triángulo
Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triangulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo ABC.


Ejemplo:
Hallar las medidas de los segmentos a y b.



Aplicaciones del teorema de Thales
El teorema de Thales se utiliza para dividir un segmento en varias partes iguales.
Ejemplo:
Dividir el segmento AB en 3 partes iguales.
1 Se dibuja una semirrecta de origen el extremo A del segmento.

2 Tomando como unidad cualquier medida, se señalan en la semirrecta 3 unidades de medida a partir de A

3 Por cada una de las divisiones de la semirrecta se trazan rectas paralelas al segmento que une B con la última división sobre la semirrecta. Los puntos obtenidos en el segmento AB determinan las 3 partes iguales en que se divide.

Os dejo un enlace de un vídeo sobre éste teorema :
Ejercicios de semejanza
Señala la opción correcta:
1Dos figuras semejantes tienen...
2Dada una figura cualquiera podemos construir otra semejante a ella...
3Entre los lados de dos figuras semejantes...
4Si un segmento de 10 cm de longitud es semjante a otro de 5 cm, entonces...
5Un triángulo de lados 5 cm, 12 cm y 13 cm es semejante a otro triángulo de lados...
6La razón de proporcionalidad de los triángulos del ejercicio anterior es...
7Si tenemos un cuadrado de lado 2.5 cm y hacemos otro semejante a él aplicando una razón de proporcionalidad k = 2 el lado del nuevo cuadrado será de...
8Dado un segmento de 20 cm, construimos otro semejante a él aplicando una escala k = 0.2. Dicho segmento medirá...
9Debido a la razón de poporcionalidad, dos figuras semejantes...
10En dos figuras semejantes...
Teorema de Pitágoras
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.


Aplicaciones del teorema de Pitágoras:
1 Conociendo los dos catetos calcular la hipotenusa

Ejemplo: Los catetos de un triángulo rectángulo miden en 3 m y 4 m respectivamente. ¿Cuánto mide la hipotenusa?


2 Conociendo la hipotenusa y un cateto, calcular el otro cateto

Ejemplo: La hipotenusa de un triángulo rectángulo mide 5 m y uno de sus catetos 3 m. ¿Cuánto mide otro cateto?


3 Conociendo sus lados, averiguar si es rectángulo
Para que sea rectángulo el cuadrado de lado mayor ha de ser igual a la suma de los cuadrados de los dos menores.
Ejemplo: Determinar si el triángulo es rectángulo.


Os dejo también un vídeo para que se lo pongáis a los niños.
Ejercicios del teorema de Pitágoras
Resuelve los siguientes problemas:
1La hipotenusa de un triángulo rectángulo mide 29 cm y uno de sus catetos mide 20 cm. ¿Cuál es la medida del otro cateto?
cm
2Tenemos dos triángulos. Un triángulo ABC cuyas medidas son 8, 15 y 17 y otro DEF de medidas 7,23 y 25. Escribe sí o no para indicar si los triángulos son o no rectángulos.
ABC 

DEF 

3Una escalera de 7.3 m de altura se apoya con el pie a 4.8 m de la pared para arreglar un problema que hay en la azotea de una casa. ¿A qué altura se encuentra la azotea?
4Las medidas de los catetos de un triángulo rectángulo son 9 y 12 cm respectivamente. ¿Cuál es la medida de la hipotenusa? Redondea a dos cifras decimales
h = cm.
Calcula las proyecciones m y n, de los catetos sobre la hipotenusa, usando el teorema del cateto y el de la altura respectivamente.Redondea a dos cifras decimales caso de ser necesario.
n = cm.
m = cm.
5Para instalar una antena parabólica se utiliza un poste sujeto por dos cables como indica la figura.
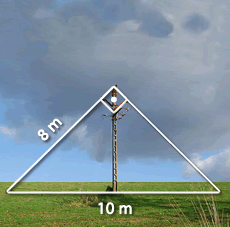
¿Cuál es la altura del poste? m.
Indica la medida del cable que falta. m.
¿A qué distancia del poste habrá que colocar dicho cable? m.
¿Qué son las escalas y cómo se representan?
La escala es la relación matemática entre las dimensiones reales de un objeto y las dimensiones de su reproducción o representación, se suele utilizar mucho en los mapas topograficos.
Pincha en el enlace para ver el vídeo que te explica las escalas:
Suscribirse a:
Entradas (Atom)













