Conceptos matemáticos de Geometría
Definición:
La geometría es una parte de la matemática que se
encarga de estudiar las propiedades y las medidas de una figura en un plano o en un espacio. Para
representar distintos aspectos de la realidad, la geometría apela a los
denominados sistemas formales o axiomáticos (compuestos
por símbolos que se unen respetando reglas y que
forman cadenas, las cuales también pueden vincularse entre sí) y a nociones
como rectas, curvas y puntos, entre otras.
Hay que
dejar patente que la geometría es una de las ciencias más antiguas que existen
en la actualidad pues sus orígenes ya se han establecido en lo que era el
Antiguo Egipto. Así, gracias a los trabajos de importantes figuras como
Heródoto o Euclides, hemos sabido que desde tiempos inmemoriales aquella estaba
muy desarrollada pues era fundamental para el estudio de áreas, volúmenes y
longitudes.
Asimismo
tampoco podemos pasar por alto que una de las figuras históricas que más han
contribuido al desarrollo de esta área científica es el matemático, filósofo y
físico francés René Descartes. Y es que este planteó el desarrollo de la
geometría de una forma en la que las distintas figuras podían ser representadas
a través de ecuaciones.
Esta
disciplina se convierte en una de las claves principales de lo que es la
asignatura de Matemáticas en los distintos centros docentes y en los distintos
niveles educativos. Así, tanto en Primaria como en Secundaria, por ejemplo, se
desarrollan lecciones que giran entorno a aquella.
En
concreto, entre las unidades que versan sobre dicha materia destacan todas
aquellas que permiten que el alumno en cuestión aprenda todos los conocimientos
necesarios sobre los elementos del plano, los polígonos, los triángulos, las
traslaciones y giros, la semejanza o las áreas y volúmenes de los cuerpos
geométricos.
Así, por
ejemplo, a la hora de desarrollar esta última lección citada los estudiantes
trabajarán sobre lo que es el prisma, el cilindro, el tetraedro, la esfera, el
cubo o el tronco de la pirámide.
La
geometría parte de axiomas (las
proposiciones que se encargan de relacionar los conceptos); estos axiomas dan
lugar a teorías que,
mediante instrumentos de esta disciplina como el transportador o el compás,
pueden comprobarse o refutarse.
Entre las
distintas corrientes de la geometría, se destaca la geometría algorítmica, que usa el álgebra y sus
cálculos para resolver problemas vinculados a la extensión.
La geometría descriptiva, por su parte, se dedica a
solucionar los problemas del espacio mediante operaciones que se desarrollan en
un plano donde están representadas las figuras de los sólidos.
La geometría analítica se encarga de estudiar las
figuras a partir de un sistema de coordenadas y de las metodologías propias del
análisis matemático.
Por
último, podemos agrupar tres ramas de la geometría con diferentes
características y alcances. La geometría proyectiva se
encarga de las proyecciones de las figuras sobre un plano; la geometría del espacio se centra en las figuras
cuyos puntos no pertenecen todos al mismo plano; mientras que la geometría plana considera las figuras que tienen
la totalidad de sus puntos en un plano.
Figuras Geométricas:
A continuación veremos los conceptos de Geometría necesarios para explicar correctamente esta parte de las Matemáticas en Primaria. Empezaremos por lo más elemental, los pintos, e iremos construyendo elementos hasta llegar a los polígonos, a los que dedicaremos un poco más de espacio.
- Puntos, rectas, planos
En el campo de la geometría plana existen tres conceptos, a los que se les llaman conceptos primitivos, que no tienen definición, pues no existe una palabra más sencilla para expresarlos; tales conceptos son: punto, recta y plano
NOCIÓN DE UN PUNTO
- La marca que deja un lápiz afilado.
- La cabeza de un alfiler.
- El lugar donde se cruzan dos hilos.
- Un grano de arena.
- ¿Cuál es la representación geométrica de un punto?Usualmente, cuando se habla de puntos y se quiere representarlos en papel y lápiz, se suele dibujar una “bolita rellena”.
- Un punto no tiene dimensión (tamaño).
- Sirve para indicar una posición.
- Se nombran con una letra mayúscula: A B C
PUNTOS IMPORTANTES
Dos puntos determinan una recta.
Tres puntos determinan un plano.
La intersección de dos planos es una recta.
La intersección de dos rectas es un punto.
Los puntos, rectas y planos no tienen grosor.
TIPOS DE PUNTOS:
Puntos Colineales o alineados
Son aquellos que están sobre la misma línea o recta.
Puntos no colineales
Son aquellos que no están sobre la misma línea o recta.
Puntos coplanares
Son aquellos puntos que están en un mismo plano
Puntos no coplanares
Son aquellos que no están en un mismo plano.
NOCIÓN DE UNA RECTA
- Un hilo extendido y tenso.
- Las intersecciones de las caras de una caja.
- El borde de una página de un libro.
- ¿ Cuál es la representación geométrica de una recta?
- Usualmente, cuando se habla de rectas y se quiere representarlas en papel y lápiz, se suele dibujar una “raya”; con un par de flechas en sus extremos; las flechas quieren dar a entender que las rectas son infinitas.
TIPOS DE RECTAS:
Los planos se suelen representar por medio de cuadrados, rectángulos o romboides. Se denotan por medio de una letra del alfabeto griego o por tres letras, que corresponden a tres de sus puntos dibujados en su representación.
- Espacio:
Un plano es una
superficie con dichas características o un adjetivo que refiere a lo perteneciente
o relativo al plano.
En este sentido, un plano
es un elemento que sólo
cuenta con dos dimensiones y que alberga infinitos puntos y rectas.
Puede nombrarse con una letra mayúscula. Por ejemplo: “La
maestra nos pidió que ubiquemos tres puntos en el plano A y un segmento en
el plano B”, “En
el plano X, podemos ver cómo se cruzan ambas variables”.
- Segmento:
Con origen en el vocablo latino segmentum, el concepto de segmento describe a la porción de una recta que está delimitada por dos puntos. Desde la perspectiva de la geometría, una recta es
producto de la unión de infinitos segmentos y puntos; el segmento, en cambio,
sólo es una porción de recta unida por un par de puntos.
Se dice que los segmentos son consecutivos
cuando poseen un extremo en común. Si pertenecen a la misma recta se denominan segmentos colineales, de lo contrario reciben el nombre
de segmentos no colineales.
Estableciendo una tipología podemos
hablar, por tanto, de las siguientes clases de segmentos:
Segmento nulo, aquel cuyos extremos coinciden.
Segmentos consecutivos son los que tienen un extremo en común.
Segmentos adyacentes son dos segmentos consecutivos que forman parte de la
misma recta.
Asimismo tenemos que hacer referencia a lo
que se conoce como mediatriz de un segmento. La misma se define por ser la
recta que pasa por lo que es el punto medio de aquel y que además es perpendicular
al mismo.
Además de todo lo expuesto tenemos que
establecer igualmente que se pueden llevar a cabo diversas operaciones con
segmentos. Entre ellas la más frecuente es la suma que se define por ser otro
segmento que se inicia con el origen del primer segmento y que finaliza con el
final del segundo segmento. La longitud, por tanto, del llamado segmento suma
es, por tanto, la de la suma de los dos segmentos previos.
No obstante, también se puede acometer la
resta de segmentos, la multiplicación de un número por un segmento, la división
de un segmento por un número o la división de un segmento en partes.
Siguiendo en este ámbito de la geometría
no podemos pasar por alto la expresión segmento esférico. Este se define por
ser cada una de las partes en las que ha quedado dividida una esfera que ha
sido cortada por un plano que, en ningún momento, ha pasado por lo que es el
centro de la misma.
- Ángulos:
Ángulo es un concepto de la Geometría para referirse al espacio comprendido entre la intersección de dos líneas que parten de un mismo punto o vértice, y que es medido en grados. La palabra proviene del latín angŭlus, y esta a su vez del griego ἀγκύλος, que significa ‘encorvado’.
En el uso cotidiano, la palabra ángulo también puede utilizarse como sinónimo de rincón (en el sentido de ángulo entrante): “¿En qué ángulo de la sala prefieres poner el sofá?”; de esquina o arista: “Cuidado con los ángulos de la mesa: te puedes golpear”; así como de punto de vista: “¿Ya evaluaste la situación desde todos los ángulos?”
TIPOS DE ÁNGULOS:
Ángulo nulo
El ángulo nulo es aquel formado por dos líneas que coinciden en su vértice y en sus extremos, por lo tanto, su abertura es de 0°.
Ángulo agudo
El ángulo agudo es aquel con una abertura de vértice mayor de 0° y menor de 90°.
Ángulo recto
El ángulo recto se encuentra conformado por dos semirrectas cuya abertura de vértice es de 90°.
Ángulo obtuso
El ángulo obtuso es aquel cuya abertura de vértice es mayor de 90° y menor de 180°.
Ángulo llano
El ángulo llano es aquel constituido por dos semirrectas con un vértice de 180° de abertura.
Ángulo oblicuo
El ángulo oblicuo, reflejo o cóncavo, es aquel que posee un vértice de abertura superior de 180° y menor de 360°.
Ángulo complementario
El ángulo complementario es aquel que, junto con otro, suma una abertura de 90°. Puede tratarse de ángulos consecutivos o no en el espacio, pero serán complementarios siempre que la sumatoria de sus ángulos arroje 90° como resultado.
Ángulo suplementario
Como ángulo suplementario se denomina aquel que, junto con otro, suma una abertura de 180°.
- Curvas:
Tipos de curvas:
Curva simple: El lápiz no pasa dos veces por el mismo punto. Pueden ser:
- Cóncava y Convexa:
LA CIRCUNFERENCIA
EL CÍRCULO
POLÍGONOS












Tiene los 4 lados iguales y los 4 ángulos rectos.

Tiene lados iguales dos a dos y los 4 ángulos rectos.

Tiene los cuatro lados iguales.

Tiene lados iguales dos a dos.

Tiene un ángulo recto.

Tiene dos lados no paralelos iguales.

No tiene ningún lado igual ni ángulo recto.









 USO COTIDIANO DE LA GEOMETRÍA:
USO COTIDIANO DE LA GEOMETRÍA:

De igual modo podríamos mencionar la presencia de la geometría en los juegos, tanto individuales (tangram, parchís, etc.), como en los colectivos, delimitando mediante diferentes formas geométricas los campos de juego y las zonas de aplicación de las reglas para desarrollar el mismo.

EJERCICIOS DE GEOMETRÍA:
Aquí os dejo unos ejercicios de geometría para que los niños practiquen y unas webs para que lo hagan de forma on-line:
Geometría. El Rincón del maestro
Educapeques.Ejercicios de figuras geometricas para primaria
mates/geometria/castella/

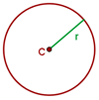
La circunferencia es una línea curva cerrada cuyos puntos están todos a la misma distancia de un punto fijo llamado centro.
Elementos de la circunferencia
Centro de la circunferencia
El centro es el punto del que equidistan todos los puntos de la circunferencia.
Radio de la circunferencia
El radio es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma.
Cuerda
Diámetro
Arco
Semicircunferencia
EL CÍRCULO
POLÍGONOS
Un polígono es una figura plana con lados rectos.
¿Es un polígono?
Los polígonos son formas bidimensionales. Están hechos con líneas rectas, y su forma es "cerrada" (todas las líneas están conectadas).
 |  |  |
| Polígono (lados rectos) | No es un polígono (tiene una curva) | No es un polígono (abierto, no cerrado) |
Tipos de polígonos
Simple o complejo
Un polígono simple sólo tiene un borde que no se cruza con él mismo. ¡Uno complejo se interseca consigo mismo!
 | 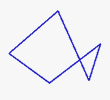 |
| Polígono simple (este es un pentágono) | Polígono complejo (también es un pentágono) |
Cóncavo o convexo
Un polígono convexo no tiene ángulos que apunten hacia dentro. En concreto, los ángulos internos no son mayores que 180°.
Si hay algún ángulo interno mayor que 180° entonces es cóncavo. (Para acordarte: cóncavo es como tener una "cueva")
 |  |
| Convexo | Cóncavo |
Regular o irregular
Si todos los ángulos son iguales y los lados también, es regular, si no es irregular
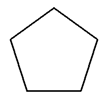 |  |
| Regular | Irregular |
Más ejemplos
 |  | 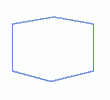 |
| Polígono complejo (un "polígono estrellado", en este caso un pentagrama) | Octágono cóncavo | Hexágono irregular |
Nombres de polígonos
| Si es regular... | |||
| Nombre | Lados | Forma | Ángulo interior |
|---|---|---|---|
| Triángulo (o trígono) | 3 | 60° | |
| Cuadrilátero (o tetrágono) | 4 | 90° | |
| Pentágono | 5 | 108° | |
| Hexágono | 6 | 120° | |
| Heptágono (o Septágono) | 7 | 128.571° | |
| Octágono | 8 | 135° | |
| Nonágono (or eneágono) | 9 | 140° | |
| Decágono | 10 | 144° | |
| Endecágono (or undecágono) | 11 | 147.273° | |
| Dodecágono | 12 | 150° | |
Triángulos
Un triángulo es un polígono de tres lados.
Un triángulo está determinado por tres segmentos de recta que se denominanlados, o por tres puntos no alineados llamados vértices.


Propiedades del triángulo
1 Un lado de un triángulo es menor que la suma de los otros dos y mayor que su diferencia.
a < b + c
a > b - c
2La suma de los ángulos interiores de un triángulo es igual a 180°.
A + B + C =180º
Tipos de triángulos según sus lados
Triángulo equilátero

Tres lados iguales.
Triángulo isósceles

Dos lados iguales.
Triángulo escaleno

Tres lados desiguales.
Tipos de triángulos según sus ángulos
Triángulo acutángulo

Tres ángulos agudos
Triángulo rectángulo

Un ángulo recto
El lado mayor es la hipotenusa.
Los lados menores son los catetos.
Triángulo obtusángulo

Un ángulo obtuso.
Triángulos iguales
1Dos triángulos son iguales cuando tienen iguales un lado y sus dos ángulos adyacentes.
2Dos triángulos son iguales cuando tienen dos lados iguales y el ángulo comprendido.
3Dos triángulos son iguales cuando tienen los tres lados iguales.
Perímetro del triangulo
El perímetro del triangulo es igual a la suma de las longitudes de sustres lados.
Perímetro del triangulo equilátero
Perímetro del triangulo isósceles
Perímetro del triangulo escaleno
Área de un triángulo
El área de un triángulo es igual a base por altura partido por 2.
La altura es la recta perpendicular trazada desde un vértice al lado opuesto (o su prolongación).
Área de un triángulo equilátero
Área de un triángulo rectángulo
El área de un triángulo rectángulo es igual al producto de los catetos partido por 2.


Propiedades de los triángulos
1Un lado de un triángulo es menor que la suma de los otros dos y mayor que su diferencia.Propiedades
2 La suma de los ángulos interiores de un triángulo es igual a 180°.
3 El valor de un ángulo exterior es igual a la suma de los dos interiores no adyacentes.
Elementos de los triángulos
Alturas de un triángulo
Altura es cada una de las rectas perpendiculares trazadas desde un vértice al lado opuesto (o su prolongación).
Ortocentro
Es el punto de corte de las tres alturas.

Medianas de un triángulo
Mediana es cada una de las rectas que une el punto medio de un lado con el vértice opuesto.
Baricentro
Mediatrices de un triángulo
Mediatriz es cada una de las rectas perpendiculares trazadas a un lado por su punto medio.
Circuncentro
Bisectrices de un triángulo
Bisectriz es cada una de las rectas que divide a un ángulo en dos ángulos iguales.
Incentro
Recta de Euler
Cuadriláteros
Un cuadrilátero es un polígono de cuatro lados.
La suma de sus ángulos interiores de un cuadrilátero es igual a 360°.
Hay tres tipos de cuadriláteros:
Paralelogramos.
Trapecios.
Trapezoides.
Paralelogramos
Un paralelogramo es un cuadrilátero que tienen los lados paralelos dos a dos. Se clasifican en:
Cuadrado

Tiene los 4 lados iguales y los 4 ángulos rectos.
Rectángulo

Tiene lados iguales dos a dos y los 4 ángulos rectos.
Rombo

Tiene los cuatro lados iguales.
Romboide

Tiene lados iguales dos a dos.
Trapecios
Un trapecio es un cuadrilátero que tienen dos lados paralelos, llamados base mayor y base menor. Se clasifican en:
Trapecio rectángulo

Tiene un ángulo recto.
Trapecio isósceles

Tiene dos lados no paralelos iguales.
Trapecio escaleno

No tiene ningún lado igual ni ángulo recto.
Trapezoides
Un trapezoide es un cuadrilátero que no tiene ningún lado igual ni paralelo

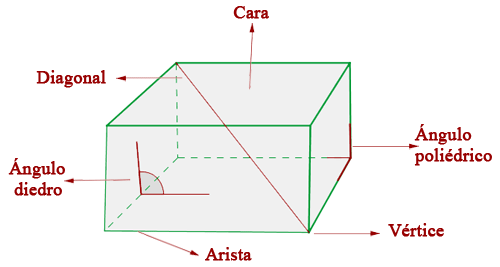
Poliedros
Un poliedro es la región del espacio limitada por polígonos.

Caras
Las caras de un poliedro son cada uno de los polígonos que limitan alpoliedro.
Aristas
Las aristas de un poliedro son los lados de las caras del poliedro. Dos caras tienen una arista en común.
Vértices
Los vértices de un poliedro son los vértices de cada una de las carasdel poliedro. Tres caras coinciden en un mismo vértice.
Ángulos diedros
Los ángulos diedros están formados por cada dos caras y tienen unaarista en común.
Ángulos poliédricos
Los ángulos poliédricos están formados por tres o más caras delpoliedro y tienen un vértice común.
Diagonales
Las diagonales de un poliedro son los segmentos que unen dos vértices no pertenecientes a la misma cara.
Relación de Euler
En todos los poliedros convexos se verifica siempre que:
Nº de caras + Nº de vértices = Nº de aristas + 2.
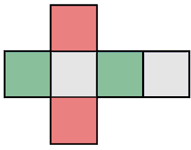
Poliedros regulares:
Los poliedros regulares tiene todos sus ángulos diedros y todos sus ángulos poliedros iguales y sus caras son polígonos regulares iguales.
Sólo hay cinco poliedros regulares.
Tetraedro


Su superficie está formada por 4 triángulos equiláteros iguales.
Tiene cuatro vértices y cuatro aristas.
Hexaedro o cubo


Su superficie está constituida por 6 cuadrados.
Tiene 8 vértices y 12 aristas.
Octaedro


Su superficie consta de ocho triángulos equiláteros.
Tiene 6 vértices y 12 aristas.
Dodecaedro


Su superficie consta de 12 pentágonos regulares.
Tiene 20 vértices y 30 aristas.
Icosaedro


Su superficie consta de 20 triángulos equiláteros.
Tiene 12 vértices y 30 aristas.
En nuestra vida cotidiana es más que frecuente la utilización de diferentes conceptos geométricos, aunque la mayoría de las veces ni siquiera tomamos conciencia de este hecho. Veamos algunos ejemplos:
Desplazamientos: Mientras vamos de un lugar a otro en realidad estamos siguiendo unos recorridos basados en el desplazamiento sobre unas líneas que la mente determina a partir de nuestra situación inicial y el punto de destino final. Conceptos como longitudes, medidas de ángulos, direcciones, etc. son utilizados en cada uno de estos desplazamientos.
Superficies: A menudo expresiones como “grande”, “pequeño”, etc. no son suficientes para determinar correctamente una extensión concreta, como por ejemplo la superficie de un piso. Cuando necesitamos ser más exactos acudimos a un patrón de medida que nos permite determinar con mayor exactitud esa magnitud. Así hablamos de un piso de 60 metros cuadrados, o un terreno de 800 metros cuadrados, etc. lo que nos da una idea más precisa del tamaño.
Arte: La geometría está presente en un gran cantidad de obras pictóricas, esculturas, e incluso en diferentes piezas y ornamentos de nuestra vida cotidiana. Las figuras geométricas son un elemento habitual en fachadas, suelos y azulejos, desde “los mosaicos nazaríes” presentes en la Alambra de Granada hasta los que hoy nos podemos encontrar en cualquier calle de nuestra ciudad o fachada de cualquier casa.

En la imagen podemos ver un detalle de una fachada que incorpora diferentes electos geométricos.
De igual modo podríamos mencionar la presencia de la geometría en los juegos, tanto individuales (tangram, parchís, etc.), como en los colectivos, delimitando mediante diferentes formas geométricas los campos de juego y las zonas de aplicación de las reglas para desarrollar el mismo.
Así, podríamos continuar con una innumerable lista de ejemplos de diferentes situaciones de nuestra vida cotidiana en las que la geometría está presente, aunque posiblemente en la mayoría de los casos ya son tan familiares que las manejamos sin percatarnos de este hecho.

EJERCICIOS DE GEOMETRÍA:
Aquí os dejo unos ejercicios de geometría para que los niños practiquen y unas webs para que lo hagan de forma on-line:
Geometría. El Rincón del maestro
Educapeques.Ejercicios de figuras geometricas para primaria
mates/geometria/castella/
Actividades con geoplanos:
DESCRIPCIÓN DEL MATERIAL:
Consiste en un tablero cuadrado, generalmente de
madera, el cual se ha cuadriculado y se ha introducido un clavo en cada vértice
de tal manera que éstos sobresalen de la superficie de la madera unos 2cm. El
tamaño del tablero es variable y está determinado por un número de cuadrículas;
éstas pueden variar desde 9 (3 x 3) hasta 121 (11 x 11). El trozo de madera
utilizado no puede ser una plancha fina, ya que tiene que ser lo
suficientemente grueso -2cm aproximadamente- como para poder insertar los
clavos de modo que queden firmes y que no se ladeen. Sobre esta base se colocan
gomas elásticas de colores que se sujetan en los clavos formando las figuras
geométricas que se deseen.
ÁREA DE APLICACIÓN:
El uso del geoplano contribuye a desarrollar el
subcampo del pensamiento espacial y sistemas geométricos.
UTILIDAD Y OBJETIVOS:
·
La representación de la geometría en los primeros años de forma lúdica y
atractiva, y no como venía siendo tradicional, de forma verbal y abstracta, al
final de curso y de manera secundaria.
·
Es de fácil manejo para cualquier niño y permite el paso rápido de
una a otra actividad, lo que mantiene a los alumnos continuamente activos en la
realización de ejercicios variados.
·
Desarrollar la creatividad a través de la composición y descomposición de
figuras geométricas en un contexto de juego libre.
·
Conseguir una mayor autonomía intelectual de los niños, potenciando que,
mediante actividades libre y dirigidas con el geoplano, descubran por sí mismos
algunos de los conocimientos geométricos básicos.
·
Desarrollar la reversibilidad del pensamiento: la fácil y rápida
manipulación de las gomas elásticas permite realizar transformaciones diversas
y volver a la posición inicial deshaciendo el movimiento.
Actividades con geoplanos:
DESCRIPCIÓN DEL MATERIAL:
Consiste en un tablero cuadrado, generalmente de
madera, el cual se ha cuadriculado y se ha introducido un clavo en cada vértice
de tal manera que éstos sobresalen de la superficie de la madera unos 2cm. El
tamaño del tablero es variable y está determinado por un número de cuadrículas;
éstas pueden variar desde 9 (3 x 3) hasta 121 (11 x 11). El trozo de madera
utilizado no puede ser una plancha fina, ya que tiene que ser lo
suficientemente grueso -2cm aproximadamente- como para poder insertar los
clavos de modo que queden firmes y que no se ladeen. Sobre esta base se colocan
gomas elásticas de colores que se sujetan en los clavos formando las figuras
geométricas que se deseen.
ÁREA DE APLICACIÓN:
El uso del geoplano contribuye a desarrollar el
subcampo del pensamiento espacial y sistemas geométricos.
UTILIDAD Y OBJETIVOS:
·
La representación de la geometría en los primeros años de forma lúdica y
atractiva, y no como venía siendo tradicional, de forma verbal y abstracta, al
final de curso y de manera secundaria.
·
Es de fácil manejo para cualquier niño y permite el paso rápido de
una a otra actividad, lo que mantiene a los alumnos continuamente activos en la
realización de ejercicios variados.
·
Desarrollar la creatividad a través de la composición y descomposición de
figuras geométricas en un contexto de juego libre.
·
Conseguir una mayor autonomía intelectual de los niños, potenciando que,
mediante actividades libre y dirigidas con el geoplano, descubran por sí mismos
algunos de los conocimientos geométricos básicos.
·
Desarrollar la reversibilidad del pensamiento: la fácil y rápida
manipulación de las gomas elásticas permite realizar transformaciones diversas
y volver a la posición inicial deshaciendo el movimiento.

·
Llegar a reconocer y adquirir la noción de ángulo, vértice y lado.
·
Comparar diferentes longitudes y superficies; hacer las figuras más grandes
estirando las gomas a más cuadrículas.
·
Componer figuras y descomponerlas a través de la superposición de
polígonos.
·
Introducir la clasificación de los polígonos a partir de actividades de
recuento de lados.
·
Llegar al concepto intuitivo de superficie a través de las cuadrículas que
contiene cada polígono.
·
Introducir los movimientos en el plano; girando el geoplano se puede
observar una misma figura desde muchas posiciones, evitando el error de asociar
una figura a una posición determinada, tal es el caso del cuadrado.
·
Desarrollar las simetrías y la noción de rotación.
Actividades:
Se recomienda hacer un reconocimiento inicial
del material, tocando los puntos, contando los puntos por línea y luego el
total y representando gráficamente en una hoja los puntos del geoplano.
Luego realizar actividades libres con trabajos
sencillos como representar objetos de la vida cotidiana (una casa, una
estrella, etc.).
Se recomienda
realizar las siguientes actividades:
1. Formas geométricas
Además enseña cómo convertir una figura en otra:
2.Estirar y encoger figuras geométricas
3.Desplazamiento de figuras geométricas
4.Simetría de figuras geométricas
5.fracciones
A nivel más
avanzado se enseña a descubrir el área y el perímetro de las figuras, además a
comparar perímetros, observando que figuras con diferente forma pueden tener
igual perímetro.
EJEMPLO USO DEL GEOPLANO
A continuación las Alumnas de primero de primaria del colegio Magdalena Ortega Nariño muestran sus creaciones utilizando el geoplano.
Grupo exhibiendo diseños (Febrero 2011)
Ejemplo diseño libre (Febrero 2011)
Ejemplo diseño libre (Febrero 2011)
Actividades con
Tangram
CÓMO SE JUEGA AL TANGRAM:
El tangram chino es un rompecabezas fácil de construir puesto que se obtiene dividiendo un cuadradoen siete piezas, llamadas “tans”:
Ø 5 triángulos de diferente tamaño
Ø 1 cuadrado
Ø 1 trapecio
El juego consiste en construir figuras, utilizando todas las piezas sin sobreponerlas.
UTILIDAD:
El tangram se utiliza como entretenimiento en psicología, educación física y particularmente en pedagogía, en el área de matemáticas el tangram es un juego muy útil para introducir conceptos de geometría plana porque permite la manipulación de materiales y contribuye al desarrollo psicomotor e intelectual de los niños y las niñas.
.
Videos:
EJEMPLO USO DE TANGRAM EN CLASE
Estudiante familiarizandose con el Tangram
Estudiante dibujando las figuras del Tangram
Estudiante siguiendo instrucción para construcción de figuras
| |||||||


































































No hay comentarios:
Publicar un comentario