Introducción a las potencias y raíces y su Didáctica

Historia

Tiempo más tarde, los babilonios desarrollaron matemáticas más sofisticadas, lo cual les permitió encontrar las raíces positivas de cualquier ecuación de segundo grado. También lograron encontrar las raíces de algunas ecuaciones de tercer grado, y resolvieron problemas más complicados utilizando el teorema de Pitágoras. Fueron capaces de recopilar gran cantidad de tablas, como las de multiplicar, de dividir, de cuadrados y hasta las de interés compuesto. Calcularon la suma de progresiones aritméticas y de algunas geométricas, pero también de sucesiones de cuadrados. Aunque también obtuvieron una buena aproximación de la raíz cuadrada.

Uno de los grupos más innovadores en la historia de las matemáticas fueron los egipcios, quienes inventaron las matemáticas abstractas basadas en definiciones, axiomas y demostraciones. Los descubridores egipcios más importantes fueron Tales de Mileto y Pitágoras de Samos, quien explicó la importancia del estudio de los números para poder entender el mundo.

Conceptos:

En el Curriculum de Primaria sólo se hace referencia a las potencias de 10 en 5º y 6º .

Vamos a explicar en qué consisten las potencia y, por ende, las raíces para tener una ligera idea de qué son aunque realmente en los centros estas últimas como tal no aparecen explícitamente.

El nivel en el que se ven estos conceptos en la Educación Primaria es muy elemental pero aparecen en todos los libros de texto.

Potencia
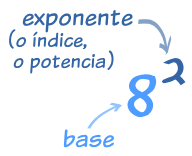	La potencia de un número muestra cuántas veces se usa el número en una multiplicación. Se escribe como un número pequeño a la derecha y arriba del número base. En este ejemplo: 82 = 8 × 8 = 64 (Otros nombres para potencia son índice o exponente)

Exponentes

Los exponentes también se llaman potencias o índices

El exponente de un número nos dice cuántas veces se usa el número en una multiplicación. En este ejemplo: 82 = 8 × 8 = 64 En palabras: 82 se puede leer "8 a la segunda potencia", "8 a la potencia 2" o simplemente "8 al cuadrado"

Más ejemplos:

Ejemplo: 5³ = 5 × 5 × 5 = 125

• En palabras: 5³ se puede leer "5 a la tercera potencia", "5 a la potencia 3" o simplemente "5 al cubo"

Ejemplo: 2⁴ = 2 × 2 × 2 × 2 = 16

• En palabras: 2⁴ se puede leer "2 a la cuarta potencia" or "2 a la potencia 4" o simplemente "2 a la cuarta"

Y los exponentes hacen más fácil escribir muchas multiplicaciones

Ejemplo: 9⁶ es más fácil de escribir y leer que 9 × 9 × 9 × 9 × 9 × 9

Puedes multiplicar cualquier número por sí mismo tantas veces como quieras con esta notación.

Así que, en general:

an te dice que multipliques a por sí mismo, y hay n de esos a's: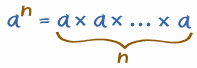

Exponentes negativos

¿Negativos? ¿Qué es lo contrario de multiplicar? ¡Dividir! Un exponente negativo significa cuántas veces se divide entre el número.

Ejemplo: 8^-1 = 1 ÷ 8 = 0,125

O varias divisiones:

Ejemplo: 5^-3 = 1 ÷ 5 ÷ 5 ÷ 5 = 0,008

Pero esto lo podemos hacer más fácilmente:

5^-3 también se podría calcular así:

1 ÷ (5 × 5 × 5) = 1/5³ = 1/125 = 0,008

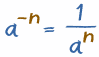Este último ejemplo nos muestra una manera más fácil de manejar exponentes negativos: Calcula la potencia positiva (an) Después cacula el recíproco (o sea 1/an)

Más ejemplos:

Exponente negativo		Recíproco del exponente positivo		Respuesta
4-2	=	1 / 42	=	1/16 = 0,0625
10-3	=	1 / 103	=	1/1.000 = 0,001

¿Qué pasa si el exponente es 1 o 0?

Si el exponente es 1, entonces tienes el número solo (por ejemplo 9¹ = 9)

Si el exponente es 0, la respuesta es 1 (por ejemplo 9⁰ = 1)

Tiene sentido

Mi método favorito es empezar con "1" y multiplicar y o dividir tantas veces como diga el exponente, y tendrás la respuesta correcta, por ejemplo:

Ejemplo: potencias de 5
	... etc...
52	1 × 5 × 5	25
51	1 × 5	5
50	1	1
5-1	1 ÷ 5	0,2
5-2	1 ÷ 5 ÷ 5	0,04
	... etc...

Si miras esta tabla, verás que los exponentes positivos, cero y negativos son en realidad parte de un mismo (y bastante sencillo) patrón.

Leyes de los exponentes

Todo lo que necesitas saber...

Todas las "Leyes de los Exponentes" (o también "reglas de los exponentes") vienen de tres ideas:

	El exponente de un número dice multiplica el número por sí mismo tantas veces
	Lo contrario de multiplicar es dividir, así que un exponente negativo significa dividir
	Un exponente fraccionario como 1/n quiere decir hacer la raíz n-ésima:

Si entiendes esto, ¡entonces entiendes todos los exponentes!

Y todas las reglas que siguen se basan en esas ideas.

Leyes de los exponentes

Aquí están las leyes (las explicaciones están después):

Ley	Ejemplo
x1 = x	61 = 6
x0 = 1	70 = 1
x-1 = 1/x	4-1 = 1/4
xmxn = xm+n	x2x3 = x2+3 = x5
xm/xn = xm-n	x4/x2 = x4-2 = x2
(xm)n = xmn	(x2)3 = x2×3 = x6
(xy)n = xnyn	(xy)3 = x3y3
(x/y)n = xn/yn	(x/y)2 = x2 / y2
x-n = 1/xn	x-3 = 1/x3

Explicaciones de las leyes

Las tres primeras leyes (x¹ = x, x⁰ = 1 y x^-1 = 1/x) son sólo parte de la sucesión natural de exponentes. Mira este ejemplo:

Ejemplo: potencias de 5
	... etc...
52	1 × 5 × 5	25
51	1 × 5	5
50	1	1
5-1	1 ÷ 5	0,2
5-2	1 ÷ 5 ÷ 5	0,04
	... etc...

verás que los exponentes positivos, cero y negativos son en realidad parte de un mismo patrón, es decir 5 veces más grande (o pequeño) cuando el exponente crece (o disminuye).

La ley que dice que x^mxⁿ = x^m+n

En x^mxⁿ, ¿cuántas veces multiplicas "x"? Respuesta: primero "m" veces, despuésotras "n" veces, en total "m+n" veces.

Ejemplo: x²x³ = (xx) × (xxx) = xxxxx = x⁵

Así que x²x³ = x⁽²⁺³⁾ = x⁵

La ley que dice que x^m/xⁿ = x^m-n

Como en el ejemplo anterior, ¿cuántas veces multiplicas "x"? Respuesta: "m" veces, después reduce eso"n" veces (porque estás dividiendo), en total "m-n" veces.

Ejemplo: x^4-2 = x⁴/x² = (xxxx) / (xx) = xx = x²

(Recuerda que x/x = 1, así que cada vez que hay una x "sobre la línea" y una "bajo la línea" puedes cancelarlas.)

Esta ley también te muestra por qué x⁰=1 :

Ejemplo: x²/x² = x^2-2 = x⁰ =1

La ley que dice que (x^m)ⁿ = x^mn

Primero multiplicas x "m" veces. Después tienes que hacer eso "n" veces, en total m×n veces.

Ejemplo: (x³)⁴ = (xxx)⁴ = (xxx)(xxx)(xxx)(xxx) = xxxxxxxxxxxx = x¹²

Así que (x³)⁴ = x^3×4 = x¹²

La ley que dice que (xy)ⁿ = xⁿyⁿ

Para ver cómo funciona, sólo piensa en ordenar las "x"s y las "y"s como en este ejemplo:

Ejemplo: (xy)³ = (xy)(xy)(xy) = xyxyxy = xxxyyy = (xxx)(yyy) = x³y³

La ley que dice que (x/y)ⁿ = xⁿ/yⁿ

Parecido al ejemplo anterior, sólo ordena las "x"s y las "y"s

Ejemplo: (x/y)³ = (x/y)(x/y)(x/y) = (xxx)/(yyy) = x³/y³

La ley que dice que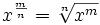 

Para entenderlo, sólo recuerda de las fracciones que n/m = n × (1/m):

Ejemplo: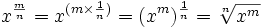 

Y eso es todo

Si te cuesta recordar todas las leyes, acuérdate de esto: siempre puedes calcular todo si entiendes las tres ideas de la parte de arriba de esta página.

Ah, una cosa más... ¿Qué pasa si x= 0?

Exponente positivo (n>0)	0n = 0
Exponente negativo (n<0)	¡No definido! (Porque dividimos entre 0)
Exponente = 0	Ummm ... ¡lee más abajo!

El extraño caso de 0⁰

Hay dos argumentos diferentes sobre el valor correcto. 0⁰ podría ser 1, o quizás 0, así que alguna gente dice que es "indeterminado":

	x0 = 1, así que ...	00 = 1
	0n = 0, así que ...	00 = 0
	Cuando dudes...	00 = "indeterminado"

Notación de índices - Potencias de 10

(Nota: índice, potencia o exponente significan todos lo mismo)

El índice de un número te dice cuántas veces usas el

número en una multiplicación.

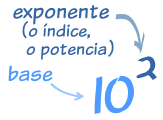Esto quiere decir 10 × 10 (el 10 se usa 2 veces en la multiplicación)

Ejemplo 1: 10³ = 10 × 10 × 10 = 1.000

• Con palabras: 10³ se podría llamar "10 a la tercera potencia", "10 a la 3" o simplemente "10 cubo"

Ejemplo 2: 10⁴ = 10 × 10 × 10 × 10 = 10.000

• Con palabras: 10⁴ se podría llamar "10 a la cuarta potencia", "10 a la potencia 4" o simplemente "10 a la 4"

Puedes multiplicar cualquier número por sí mismo tantas veces como quieras con esta notación (ver exponentes), pero las potencias de 10 tienen una utilidad especial...

Potencias de 10

Las "potencias de 10" son una manera muy útil de escribir números muy grandes.

En lugar de muchos ceros, puedes poner qué potencia de 10 necesitas para hacer todos esos ceros

Ejemplo: 5.000 = 5 × 1.000 = 5 × 10³

• Cinco mil es 5 veces mil. Y mil es 10³. Así que 5 × 10³ = 5.000
• ¿Ves cómo 10³ es una manera cómoda de escribir 3 ceros?

Científicos e ingenieros (quienes a veces usan números muy grandes o muy pequeños) encuentran muy útil esta manera de escribir números como:

• 9,46 x 10¹⁵ metros (la distancia que la luz viaja en un año), o
• 1,9891 x 10³⁰ kg (la masa del Sol).

Así evitan tener que escribir muchos ceros. Se suele llamar notación científica, o forma estándar.

Aunque parezca difícil al principio, hay un sencillo "truco":

El índice de 10 dice

cuántas posiciones se mueve el punto decimal a la derecha.

Ejemplo: ¿Cuánto es 1,35 × 10⁴ ?

Lo puedes calcular así: 1,35 x (10 × 10 × 10 × 10) = 1,35 x 10.000 = 13.500

Pero es más fácil pensar en "mover el punto decimal 4 posiciones a la derecha" así:

Potencias negativas de 10

¿Negativas? ¿Qué es lo contrario de multiplicar? ¡Dividir!

Una potencia negativa significa cuántas veces se divide por el número.

¡Los exponentes negativos van en la dirección contraria!

Ejemplo: 5 × 10^-3 = 5 ÷ 10 ÷ 10 ÷ 10 = 0,005

Sólo tienes que recordar que para potencias negativas de 10:

Para las potencias negativas de 10, mueve el punto decimal a la izquierda.

Ejemplo: ¿Cuánto es 7,1 × 10^-3?

Bueno, en realidad 7,1 x (1/10 × 1/10 × 1/10) = 7,1 x 0,001 = 0,0071

Pero es más fácil pensar en "mover el punto decimal 3 posiciones a la izquierda" así:

Resumen

El índice de 10 dice cuántas veces se mueve el punto decimal. Positivo es a la derecha, negativo a la izquierda. Ejemplo:

	Número	En notación científica	Con palabras
Potencias positivas	5.000	5 × 103	5 miles
Potencias negativas	0,005	5 × 10-3	5 milésimos

Raíz
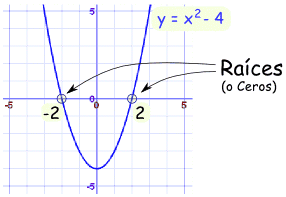	Donde una función vale cero. En este Ejemplo, -2 y 2 son las raíces de la función x2 - 4 Pero algunas veces "raíz" es usada como una manera rápida de decir "raíz cuadrada".

Raíz Cuadrada
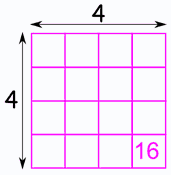	La raíz cuadrada de un número es ese valor especial que, cuando se lo multiplica por sí mismo, nos da el número. Ejemplo: 4 × 4 = 16, entonces la raíz cuadrada de 16 es 4. Su símbolo es &radic Ejemplo: √36 = 6 (porque 6 x 6 = 36)

Cuadrados y raíces cuadradas

Para entender las raíces cuadradas primero tienes que entender los cuadrados...

Cómo se calcula el cuadrado de un número

Para calcular el cuadrado de un número, sólo hay que multiplicarlo por sí mismo...

Ejemplo: ¿Cuál es el cuadrado de 3?

3 al cuadrado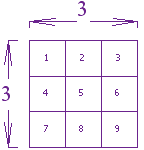

=

=

3 × 3

=

9

Nota: escribimos "3 al cuadrado" como 3²

(el "²" pequeño significa que el número aparece dos veces en la multiplicación)

Más cuadrados

4 al cuadrado	=	42	=	4 × 4	=	16
5 al cuadrado	=	52	=	5 × 5	=	25
6 al cuadrado	=	62	=	6 × 6	=	36

Raíz cuadrada

La raíz cuadrada va en la dirección contraria:

3 al cuadrado es 9, así que la raíz cuadrada de 9 es 3

3

9

La raíz cuadrada de un número es...

... ese valor particular tal que cuando lo multiplicas por sí mismo te da el número original.

La raíz cuadrada de 9 es ...

... 3, porque cuando multiplicas 3 por sí mismo sale 9.

Nota: cuando veas "raíz" piensa "conozco el árbol, pero ¿cuál es la raíz que lo produce?" En este caso el árbol es "9", y la raíz es "3".

Aquí tienes más cuadrados y raíces cuadradas:

4		16
5		25
6		36

Ejemplo: ¿Cuál es la raíz cuadrada de 25?

Bueno, acabamos de ver que 25 = 5 × 5, así que si multiplicas 5 por sí mismo (5 × 5) sale 25.

Entonces la respuesta es 5

El símbolo de raíz cuadrada

Este es el símbolo que significa "raíz cuadrada", es como una marca de "correcto", de hecho hace cientos de años empezó siendo un punto con un palito hacia arriba. Se le llama radical, ¡y siempre hace que las matemáticas parezcan importantes!

Se usa así: 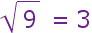 (se dice que "la raíz cuadrada de 9 es 3")

Abajo hay temas más avanzados

También puedes calcular el cuadrado de números negativos

Mira esto:

El cuadrado de 5 es 25:		5 × 5 = 25
Pero el cuadrado de -5 también es 25:		-5 × -5 = 25
(porque negativo por negativo es positivo)

Así que la raíz cuadrada de 25 puede ser 5 o -5

¡Hay una respuesta positiva y otra negativa para una raíz cuadrada!

Pero cuando la gente habla de "la" raíz cuadrada normalmente se refieren a la positiva.

Y cuando usas el símbolo radical √ siempre quiere decir la raíz positiva.

Ejemplo: √36 = 6 (no -6)

Cuadrados perfectos

Los cuadrados perfectos son los cuadrados de los números enteros:

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	etc
Cuadrados perfectos:	1	4	9	16	25	36	49	64	81	100	121	144	169	196	225	...

Es fácil calcular la raíz cuadrada de un cuadrado perfecto, pero es muy difícil calcular otras raíces cuadradas.

Ejemplo: ¿cuál es la raíz cuadrada de 10?

Bueno, 3 × 3 = 9 y 4 × 4 = 16, así que podemos adivinar que la respuesta está entre 3 y 4.

• Probamos 3.5: 3.5 × 3.5 = 12.25
• Probamos 3.2: 3.2 × 3.2 = 10.24
• Probamos 3.1: 3.1 × 3.1 = 9.61

Así vamos muy despacio... en este punto, saco mi calculadora y veo que sale:

3.1622776601683793319988935444327

... pero las cifras siguen y siguen, sin patrón. ¡Así que incluso la respuesta de la calculadora es sólo una aproximación!

(Para saber más: este tipo de números se llaman radicales y son un tipo especial de números irracionales) 

Un método especial para calcular una raíz cuadrada

Hay muchas maneras de calcular una raíz cuadrada, pero mi favorita es una muy sencilla que da una respuesta más exacta cuantas más veces se usa:

a) empieza adivinando (digamos 4 para la raíz cuadrada de 10)

b) divide entre tu aproximación (10/4 = 2.5)

c) suma eso a la aproximación (2.5+4=6.5)

d) y divide eso entre 2, o sea calcula la mitad. (6.5/2 = 3.25)

e) ahora, ese esa tu nueva aproximación, empieza otra vez en b)

... así que nuestro primer intento nos lleva de 4 a 3.25

Otra vez (de b a e) nos da: 3.163

Otra vez (de b a e) nos da: 3.1623

Así que después de hacerlo tres veces la respuesta es 3.1623, que está muy bien, porque:

3.1623 x 3.1623 = 10.00014

Es divertido hacer esto ... ¿por qué no lo usas para calcular la raíz cuadrada de 2?

EJERCICIOS PARA PRACTICAR:

Os dejo algunos ejercicios para practicar en casa con lápiz y papel y unos links para que de forma interactiva podáis realizar actividades de este tema

Potencias y raíces

Potencias y raíces de sexto

ACTIVIDADES.

1. ¿Qué es una potencia? ¿Cómo se denominan cada uno de sus términos?

2. Representa y nombra las siguientes potencias:

1. 3  . 3
2. 5  .  5  .  5
3. 4  .  4  .  4  .  4  .  4    
4. 6  .  6  .  6  .  6  .  6  .   6
5. 9  . 9  .  9  .  9  .  9  .  9  .  9  .   9  .  9
6. 8  .  8  .  8  .  8

3. ¿A qué es igual la potencia de un producto y de un cociente? Pon un ejemplo.

4. ¿Cómo se calcula el producto y el cociente de potencias de la misma base?  Pon un ejemplo.

5. ¿A qué es igual la potencia de exponente uno?  Pon un  ejemplo.

6. ¿Cómo se calculan las potencias de exponente cero?  Pon un ejemplo

7. ¿Qué es una potencia de base 10? Pon un ejemplo.

8. ¿Cómo se calcula la potencia  de una potencia?  Pon un ejemplo.

9. Calcula el resultado de las siguientes potencias:

          a.      23                                                                                          c.         35                              

          b.     73                                                                                      d.         24

   

10. Resuelve  las siguientes expresiones:

1. 25  .  23                                                                            g.        ( 64 )3
2. ( 34 )6                                                                                                            h.        35   :   33
3. 53   ·    54                                                                                                       i.         45    ·   4   :   43
4. ( 5  ·  7 )3                                                                                                  j.         105   ·   102   :    104
5. 72   ·   73                                                                                              k.         23   ·   32   ·   5
6. ( 9  ·  7 )3                                                                                    l.          6   ·   ( 10 – 8 )3

11. Calcula el valor de las siguientes expresiones:

1. 30  +  32                                                                          d.       206   :    206
2. 22   .  20                                                                          c.       43   -  42                                    

12. Calcula el resultado de las siguientes expresiones:

a.      4   +  33  - 5                                                               g.       62   -   52

           b.     34   -   33                                                                    h..      5   ·   43    -  6              

3. 53  :  ( 4 +  7 · 3 )  -  2                                               i.        2   ·  63  +   2  ·  63   +   2   ·  63
4. 3   ·   72   -  82                                                              j.        63   -   5  ·  ( 33  -  2 )

           e.      6   ·  43   -   2   ·   43                                                 k.        2     ·  103  +  5  ·  103  +  3  ·  103

           f.      2   .  52  +  3  ·  52                                                     l.        26   ·  103  //    53   ·  24

13. Resuelve las siguientes operaciones:

          a.       67  ·  65  :  63                                                                  g.       [ ( 11 · 3 )6 ]7  :  33

          b.      ( 10 : 2 )7  :  54                                                         h.       103  :  23

          c.      1215 :  12  ·  1215                                                       i.       93  :   34      

          d.      ( 383)4  :  385                                                                 j.       53  :  251

          e.      ( 30 ·  2 )10  ·  605                                                     k.      122  ·  62

          f.       ( 492 )2  · 49                                                             l.      126  ·  82

14. ¿Qué es la raíz cuadrada? Indica cómo se denominan cada uno de sus términos.

15. ¿Qué son los cuadrados perfectos?

16. ¿Qué es una raíz cuadrada entera?  Pon un ejemplo.

17. ¿Cómo se efectúa el cálculo de la raíz cuadrada de un número natural?

18. Calcula las raíces de los siguientes cuadrados perfectos: 81,  121,  144,  625,   2.704,   15.129.

19. Calcula el valor del lado de un cuadrado cuya superficie es de  289 cm.

20. La raíz cuadrada de un número es 9 y el resto es 13. ¿Cuál es el radicando?

21. Calcula las raíces de los siguientes números naturales: 256,  441,  1.225,  4.728,  574.634,  2.025,   12.568  y   1.369.

22. Efectúa las siguientes operaciones:

1. 32  +  ( 23  -  2 )  ·  5                                                  i.        24  -  23   +  22  -  2
2. ( 52  -  1 )  :    144                                                      j.        100   :  5  +  32  :  3
3. 23  ( 25   -  3 )                                                            k.       7  ·  ( 5 + 3 )  -  52  ·  4
4. (  81  -  3  )  :  2                                                          l.        12  -  18  :  2  +  4  ·   121
5. 52  +  122  :  23                                                           m.       49  +  3  ·  ( 12 – 7 )
6. ( 12  +  9  )   :   25                                                      n.        8  ·  ( 12 – 5 )  +  25
7. 32  ·  42  :  62                                                               ñ.        52  ·   ( 3 + 28 : 4 )
8. 81   :   (  16  +  5 )                                                      o.        42  :  23  +  64  :  2

23. Escribe y calcula el resultado de las siguientes potencias:

1. Potencia de base 3 y exponente 5
2. 4 elevado al cubo.
3. Dos elevado a la sexta potencia.
4. 23  +  34   -  22   +  40
5. 34  .  33  :  35
6. 34   -  23  :  22
7. [ ( 33 )2 ]0                                                           

24. Copia en tu cuaderno y completa la siguiente tabla:

a	b	a2	b2	(a – b )2	a - b
4	3
5	2
7	5
3	1

25. Reduce las siguientes expresiones:

1. a5  ·  a3                                                                                   d.       (  m2  :  m2 )  ·  m3
2. b6  :  b4                                                                                 e.        x2   ( x4  :  x2 )
3. c  ·  c5                                                                             f.        ( y3  :  y )  ·  y2

26. Calcula, por tanteo, las siguientes raíces exactas o enteras:

1. 64                                                                                   d.      191
2. 117                                                                                 e.       400
3. 125                                                                                 f.        825

27. Efectúa lo siguientes cálculos, teniendo en cuenta la prioridad de las operaciones.

              a.        52   ·   ( 3  +  28  :  4 )

              b.       34   :   9   -   22

              c.       33   ·    4   -   42

              d.       24    ·   ( 5  +  36  :  3 )

              e.       42   :   23   +   64   :   2

              f.       ( 81  :  3 )   ·   23   -   ( 42  +  3 )

              g.       24    -   23    +    22   -   2

              h.       100   :   5   +   33   :   3

              i.        7   ·   ( 5 + 3 )   -   52   ·   4

              j.        12   -   18   ;   2   +   4   ·   121

              k.       72   :   (  36  +  1 )   -   22

              l.       ( 32  -   25 )   :   ( 42  - 12 )

             m.       25     :   [ (  81  - 32 )  +  42 ]

             n.        5   ·   43   -   ( 102  :  52 )   +   100

28. ¿Cómo se llevan a cabo las operaciones con potencias de números enteros.

29. ¿Cómo se efectúa la  raíz cuadrada de los números enteros.

30. Calcula el resultado de las siguientes potencias:

a.      ( - 3 )3   ·   ( - 3 )2                                                                                                       l.      ( - 5 )4

b.      ( 4 )3   ·  4                                                                                m.      ( - 2 )0

c.      ( - 2 )12   :  ( - 2 )3                                                                                                    n.      ( - 3 )2

d.      ( - 1 )4   ·    ( - 1 )5   ·  ( - 1 )2                                                                             ñ.       74   :    72

e.      ( - 2 )5   ·   ( - 2 )2                                                                                                      o.      ( - 7 )5   :   ( - 7 )2   :   ( - 7 )4

f.      ( - 5 )7   :   ( - 5 )4                                                                                                        p.      ( - 10 )5

g.     ( - 8 )12   :  ( - 8 )10                                                                                                  q.       ( - 2 )1

h.     32   .   3   .   35                                                                                                                r.       ( -  17 )222   :   ( - 17 )122

i.      ( - 30 2 )5                                                                                                                            s.       ( - 8 )12   :   ( - 8 )10

j.      ( - 15 ) 80   ·   ( - 15 )8                                                                                               t.       ( - 4 )50   :   ( - 4 )12

k.     ( - 71 )327   :   ( - 71 )107                                                                                   u.       ( - 5 )10   :   ( - 5 )6

31. Completa el cuadro siguiente:

x	2 + x	3 + x	2 . x	3 . x	x2	x3
- 3
- 2
- 1
0
1
2
3

32. Efectúa las siguientes operaciones combinadas:

a.         32   +   5  -  ( - 2 )3   +     64

b.        ( - 5 )2   +   36   +  ( - 2 )4  -  33

c.         ( - 3 )2  .   ( - 2 )3   -    49   + 34  :   9

d.         62     +   ( -  2 )6    :   8   -  ( - 3 )2    .    100   +   5   .  ( 7 – 12 )

1. [ - 2  ·  ( 32 – 5 )  -  ( - 12 )  -  4  ·  10  .  5  + 9 ]  :  5
2. [ 5  ·  32  +  ( - 2 )  ·  5  +  7  ·  3 ]  :  23  -  ( 5 · 3 – 22 )

33. Cuáles  son las raíces cuadradas de los  siguientes números enteros:

1. 16                                       d.       100                                       g.        2.916
2. 144                                     e.        – 4                                       h.        289
3. 64                                       f..       121                                       i.         – 25

34. Completa la siguiente tabla:

Potencia	- 713	34	( 54 )3	- 97	- 102
Base
Exponente
Signo resultado

35. Efectúa las siguientes operaciones combinadas:

a.      7   ·  (  9  -  3 )   +  54

b.      ( 2  +  34 )  ·  40  -  4  ·  ( 72  -  5 )  +    256   :    4

c.      ( 82  -  12 )  :  4   -    81    ·  ( 42  -  7 )    -  5     ·  ( 1 -  12 )1

d.      63   ·   ( 12 – 7 )  -  1.725  :  75  -  52   ·   ( 23  -  3  -  5  -    289 )

USO COTIDIANO:

¿Para qué utilizamos habitualmente las potencias y raíces?

Cuando hablamos de logaritmos ¿Qué se nos viene a la mente? Seguramente creemos que estos simples exponentes no sirven para nada más que para resolverlos en clase y simplificarnos las potencias. Si es así, seria mejor conocerlos un poco.

Como sabemos el logaritmo de un número sobre una base, es igual al exponente al cual hay que elevar a la base para obtener dicho número. Tal como vemos en la imagen de al lado, un ejemplo que describe al logaritmo en si. 

La historia del logaritmo es interesante, John Napier fue el primero en definir y usar el termino logaritmo a través de un libro que desarrollo “,Mirifici Logarithmorum Canonis Descriptio”  el llamaba inicialmente a los logaritmos números artificiales, luego el nombre se transformo en el sentido del numero que indica una proporción. El logaritmo causo gran impacto en la ciencia, sobretodo la astronomía, ayudaba mucho en los cálculos complejos.

“Los logaritmos son números, que se descubrieron para facilitar la solución de los problemas aritméticos y geométricos, a través de esto se evitan todas las complejas multiplicaciones y divisiones transformándolo a algo completamente simple a través de la substitución de la multiplicación por la adición y la división por la sustracción. Además el calculo de las raíces se realiza también con gran facilidad.” Herry Briggs (1556-1631), astrónomo.

Los procesos de multiplicación, división, elevación a potencias y extracción de raíces entre números reales pueden simplificarse notoriamente tal como Herry Briggs lo decía, es por esto que el uso de los logaritmos sirve hasta ahora en varias ramas y con distintas utilidades, conozcamos algunas de estas:

En la Economía y la Banca: Los índices de crecimiento son exponenciales, se aplica en la demanda y oferta, asi como obtener los porcentajes de los parametros. Mientras en la banca sirve para medir el crecimiento de los depósitos de acuerdo al tiempo.

• En la Estadística: Suele aplicarse en el crecimiento de la población.

En la Publicidad: Cuando se realizan las estadísticas sobre la campaña publicitaria que se va a lanzar, se realizan cálculos matemáticos con logaritmos. Estas estadísticas definen el fracaso o éxito de la campaña.

• En la Medicina: Solo es aplicable en ciertos fenómenos tales como el resultado del experimento psicológico de Stenberg. También se aplica en la inmunología.

En la Psicología: Se utiliza en la ley de Weber-Fechner, fenómeno del estimulo y respuesta. Aquí la respuesta (R) se relaciona con el estimulo (E) mediante una ecuación donde por ejemplo E0 es el valor mínimo del estimulo que se encuentra en el sujeto. 

• En la Ingeniería Civil: Cuando se resuelven problemas específicos, siempre teniendo en cuenta una ecuación de segundo grado.

En la Biología: Es aplicado en los estudios de los efectos nutricionales de los organismos. Así como también en el calculo del PH. También en la genética, donde se utiliza la estadística y la probabilidad para saber sobre lo que un hijo heredara de sus padres.

• En la Geología: Sirven de cálculo para calcular la intensidad de un evento, así como un sismo o un terremoto. Aquí es usado en la escala de Richter, donde la intensidad de un sismo se conoce en base a los logaritmos.

• En la Astronomía: Para determinar la magnitud estelar de una estrella o planeta se usan cálculos de carácter logarítmico para determinar la brillantez y magnitud.  Al establecer la luminosidad visible de una estrella, se opera con tablas de logaritmos en base 2.5.

• En la Química: Para calcular el PH de las sustancias se utilizan logaritmos. El PH normalmente es medido constantemente debido al efecto de las lluvias ácidas producidas por el azufre de las plantas eléctricas y fabricas.

En la Topografía: Cuando queremos determinar la altura de un edificio usando la base y el ángulo.

• En la Música: El pentagrama es una escala logarítmica ya que la altura del sonido es proporcional a la del numero de frecuencia, además ayuda a medir los grados de tonalidad ya que se pueden representar por el logaritmo en base 2.

• Uno de los casos importantes de la aplicación de logaritmos aparte de la astronomía y las demás ciencias, creo que hay que resaltar el uso de logaritmos en la música. Les dejo el siguiente vídeo donde podrán apreciar una mejor explicación mas profunda de lo que es el uso de logaritmos en esta materia. En el vídeo podemos observar la aplicación de los logaritmos con ayuda de las notas musicales y formulas que con ayuda de los logaritmos lo que nos parecerá complicado al principio lo terminamos simplificando.

En general los logaritmos son importantes en nuestra vida ya que los emplearemos conscientemente o inconscientemente en el área que nos desarrollemos ya que serán gran ayuda para resolver esas grandes ecuaciones que se nos presentaran en adelante. 

Material manipulativo

Buen material para comprender el concepto de potencia. Es un juego educativo de Mario Ramos que tiene como objetivo enseñar a calcular potencias a través de objetos y problemas de la vida cotidiana: cubos, árbol genealógico, archivos, estuches,....