Tema de fracciones y su didáctica
Historia.
Se considera que fueron los egipcios quienes usaron por primera vez las fracciones, pero sólo aquellas de la forma 1/n o las que pueden obtenerse como combinación de ellas.
Los egipcios utilizaron las fracciones cuyo numerador es 1 y cuyo denominador es 2, 3, 4,..., y las fracciones 2/3 y 3/4 y con ellas conseguían hacer cálculos fraccionarios de todo tipo.
Por su parte los babilonios desarrollaron un eficaz sistema de notación fraccionaria, que permitió establecer aproximaciones decimales verdaderamente sorprendentes. Esta evolución y simplificación del método fraccionario permitió el desarrollo de nuevas operaciones que ayudaron a la comunidad matemática de siglos posteriores a hacer buenos cálculos de, por ejemplo, las raíces cuadradas.
Para los babilónicos era relativamente fácil conseguir aproximaciones muy precisas en sus cálculos utilizando su sistema de notación fraccionaria, la mejor de que dispuso civilización alguna hasta la época del Renacimiento.
Por último, en china antigua se destaca el hecho de que en la división de fracciones se exige la previa reducción de éstas a común denominador.
Los chinos conocían bien las operaciones con fracciones ordinarias, hasta el punto de que en este contexto hallaban el mínimo común denominador de varias fracciones. . Algunas veces se adoptaron ciertas artimañas de carácter decimal para aligerar un poco la manipulación de las fracciones.
Los griegos mostraron sus grandes dotes en cuanto a geometría en algunas construcciones geométricas de segmentos cuyas longitudes representan racionales.
Ejemplo: Representación de 3/2 en la recta numérica.
1. Se trazan dos rectas perpendiculares
2. En cada recta se toman tantas longitudes de una unidad como se necesiten y ubica el denominador y lo nombra A.
3. Une con una línea el punto A con C
4. Se marca el punto B según indica el numerador de la fracción .
5. Traza una recta paralela a la recta AC que pase por B y se halla el punto D.
6. El segmento PD tiene la longitud igual a 3/2 de la unidad.
Hemos construido así el segmento cuya longitud es 3/2.

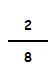
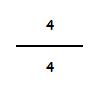
Los egipcios utilizaron las fracciones cuyo numerador es 1 y cuyo denominador es 2, 3, 4,..., y las fracciones 2/3 y 3/4 y con ellas conseguían hacer cálculos fraccionarios de todo tipo.
Por su parte los babilonios desarrollaron un eficaz sistema de notación fraccionaria, que permitió establecer aproximaciones decimales verdaderamente sorprendentes. Esta evolución y simplificación del método fraccionario permitió el desarrollo de nuevas operaciones que ayudaron a la comunidad matemática de siglos posteriores a hacer buenos cálculos de, por ejemplo, las raíces cuadradas.
Para los babilónicos era relativamente fácil conseguir aproximaciones muy precisas en sus cálculos utilizando su sistema de notación fraccionaria, la mejor de que dispuso civilización alguna hasta la época del Renacimiento.
Por último, en china antigua se destaca el hecho de que en la división de fracciones se exige la previa reducción de éstas a común denominador.
Los chinos conocían bien las operaciones con fracciones ordinarias, hasta el punto de que en este contexto hallaban el mínimo común denominador de varias fracciones. . Algunas veces se adoptaron ciertas artimañas de carácter decimal para aligerar un poco la manipulación de las fracciones.
Los griegos mostraron sus grandes dotes en cuanto a geometría en algunas construcciones geométricas de segmentos cuyas longitudes representan racionales.
Ejemplo: Representación de 3/2 en la recta numérica.
1. Se trazan dos rectas perpendiculares
2. En cada recta se toman tantas longitudes de una unidad como se necesiten y ubica el denominador y lo nombra A.
3. Une con una línea el punto A con C
4. Se marca el punto B según indica el numerador de la fracción .
5. Traza una recta paralela a la recta AC que pase por B y se halla el punto D.
6. El segmento PD tiene la longitud igual a 3/2 de la unidad.
Hemos construido así el segmento cuya longitud es 3/2.
Concepto de fracción.
La fracción se utiliza para representar las partes que se toman de un objeto que ha sido dividido en partes iguales.
Por ejemplo, dividimos una pizza en 8 partes iguales y cogemos tres. Esto se representa por la siguiente fracción:

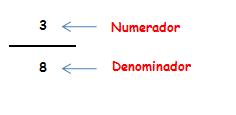
Los términos de la fracción se denominan: numerador y denominador.

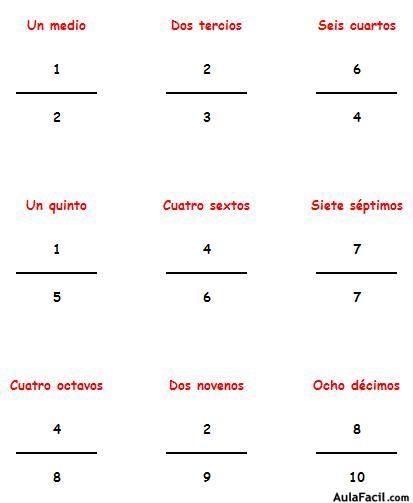
¿Cómo se leen las fracciones? Se leen en función de cuál es su denominador:
1 / 2: un medio
1 / 3: un tercio
1 / 4: un cuarto
1 / 5: un quinto
1 / 6: un sexto
1 / 7: un séptimo
1 / 8: un octavo
1 / 9: un noveno
1 / 3: un tercio
1 / 4: un cuarto
1 / 5: un quinto
1 / 6: un sexto
1 / 7: un séptimo
1 / 8: un octavo
1 / 9: un noveno
Veamos algunos ejemplos:

¿A cuantas unidades equivale una fracción? Para calcularlo se divide el numerador entre el denominador:
Por ejemplo:
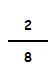
Para ver a cuantas unidades equivale esta fracción dividimos: 2 : 8 = 0,25
Equivale a 0,25 unidades
Si una fracción tiene igual numerador y denominador representa la unidad.
Por ejemplo, divido una tarta en 4 partes y me tomo las cuatro partes:
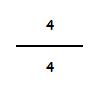
Quiere decir que me he tomado la totalidad de la tarta. (4 / 4) equivale a la unidad (a la tarta). Si dividimos 4 : 4 = 1
Fracciones equivalentes:
Las fracciones equivalentes son fracciones que representan la misma cantidad aunque parezcan diferentes. Vamos a ver un ejemplo para que nos quede más claro que significa esto:
1/2 = 2/4 = 3/6
¿Crees que es la misma cantidad? Vamos a demostrarlo ...
Como podemos ver todas las partes en color azul son iguales y todas las partes de color blanco también lo son entre sí, por tanto, podemos afirmar que todas las fracciones arriba indicadas son fracciones equivalentes porque representan la misma cantidad del círculo.
La equivalencia de las fracciones sirve para justificar teóricamente algunas de las técnicas más importantes en el cálculo con fracciones:
- Simplificar: es transformar una fracción en una fracción equivalente más simple por eso cuando simplificamos dos fracciones ponemos un "=". En realidad, estamos queriendo decir que son equivalentes.
- Fracción irreducible: es una fracción que no se puede simplificar (reducir), es decir, que el numerador y el denominador no comparten factores en común (otro que la unidad). Es la "primera" de las fracciones equivalentes a ella misma.
- Común denominador: consiste en convertirlas en otras equivalentes que tengan el mismo denominador.
- Regla de tres: encontrar uno de los términos de la proporción conocidos los otros tres ( de nuevo, el "=" que ponemos al realizar una regla de tres es en realidad una equivalencia de fracciones).
Por ejemplo:
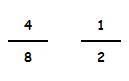
Estas dos fracciones son equivalente ya que equivalen a las mismas unidades:
4 : 8 = 0,5 unidades
1 : 2 = 0,5 unidades
¿Cómo sabemos cuando dos fracciones son equivalentes?
Para ello dividimos sus numeradores y sus denominadores, si guardan la misma proporción es que son equivalente:
Veamos un ejemplo:
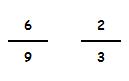
Dividimos sus numeradores: 6 : 2 = 3
Dividimos sus denominadores: 9 : 3 = 3
Guardan la misma proporción (3) luego estas dos fracciones son equivalentes.
Podemos comprobarlo.
La primera fracción equivale a 6 : 9 = 0,66 unidades
La segunda fracción equivale a 2 : 3 = 0,66 unidades
Veamos ahora un ejemplo de dos fracciones que no son equivalentes:
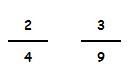
Dividimos sus numeradores: 2 : 3 = 0,66
Dividimos sus denominadores: 4 : 9 = 0,44
No guardan la misma proporción luego estas dos fracciones no son equivalentes.
Podemos comprobarlo.
La primera fracción equivale a 2 : 4 = 0,50 unidades
La segunda fracción equivale a 3 : 9 = 0,33 unidades
Comparación de fracciones:
¿Cómo puedo saber si una fracción es mayor o menor que otra?
Para ello vamos a distinguir:
- Comparar fracciones con el mismo denominador
- Comparar fracciones con distinto denominador
a) Comparar fracciones con el mismo denominador
Es mayor la fracción que tenga mayor el numerador.

Podemos comprobar que 2 / 4 = 0,5 mientras que 1 / 4 = 0,25, luego la primera fracción es mayor.
También podemos comprobar que 5 / 9 = 0,55 mientras que 3 / 9 = 0,33, luego la primera fracción es mayor.
b) Comparar fracciones con distinto denominador
En este caso puede ocurrir que tengan el mismo numerador o no.
b.1.- Si tienen el mismo numerador es mayor la que tenga menor denominador.

En este caso comprobamos que 8 / 3 = 2,66 mientras que 8 / 5 = 1,60, luego la primera fracción es mayor.
También podemos ver que 6 / 2 = 3,00 mientras que 6 / 4 = 1,50, luego la primera fracción es mayor.
b.2.- Si tienen distinto numerador entonces para poder compararlas hay que expresarlas con el mismo denominador:
Si los dos términos de una fracción se multiplican por el mismo número la fracción resultante es equivalente.
¿Y por qué número multiplicamos cada fracción? la primera fracción la multiplicamos por el denominador de la segunda, y la segunda por el denominador de la primera.
Veamos un ejemplo:
Para comparar estas dos fracciones, vamos a multiplicar los dos términos de la primera fracción por 5 ( el denominador de la segunda fracción)
Podemos comprobar que al multiplicar numerador y denominador por el mismo número la fracción no cambia: 3 / 4 = 0,75 mientras que 15 / 20 = 0,75.
Y después vamos a multiplicar los dos términos de la segunda fracción por 4 (denominador de la primera).
Las dos fracciones ya tienen el mismo denominador, luego podemos compararlas.
Ahora vemos que la segunda fracción es mayor que la primera porque su numerador es mayor.
b.3.- Si tienen distinto numerador también se pueden calcular fracciones con el mismo denominador utilizando el método del Mínimo Común Múltiplo.
Vamos a verlo con un ejemplo:
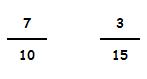
Calculamos los múltiplos de cada denominador:
Múltiplos de 10: 10, 20, 30, 40, 50, 60, 70...
Múltiplos de 15: 15, 30, 45, 60, 75, 90...
Hemos señalado en rojo el número 30 porque es un múltiplo común de ambos números y es el menor de los múltiplos comunes (por ejemplo, 60 también es un múltiplo común pero es mayor que 30).
Utilizaremos este Múltiplo Común Múltiplo como denominador común de ambas fracciones, pero para que las nuevas fracciones sean equivalentes a las anteriores tenemos que ajustar los numeradores ¿Cómo lo hacemos?
En la primera fracción vamos a sustituir su denominador 10 por 30, en definitiva, vamos a multiplicar por 3 su antiguo denominador, luego para que la fracción sea equivalente a la original tendremos también que multiplicar por 3 su numerador.
En la segunda fracción vamos a sustituir su denominador 15 por 30, por lo que vamos a multiplicarlo por 2, luego tendremos también que multiplicar por 2 su numerador.
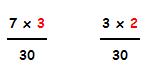
Ya podemos comparar ambas fracciones:
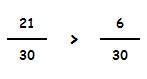
Operaciones con fracciones.
Suma y diferencia : La suma y diferencia de fracciones se justifica a partir del mismo tipo de situaciones que daban sentido a la suma y diferencia de números naturales, es decir, situaciones de parte - todo, de reunión, de transformación o de comparación. Se pueden diferenciar entre:
1.- Fracciones con igual denominador
En este caso para sumar o restar fracciones se mantiene constante el denominador y se suman o restan sus numeradores.
a) Veamos un ejemplo:
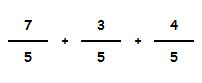
Sumamos sus numeradores y mantenemos el denominador:
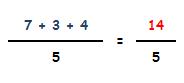
b) Veamos otro ejemplo:
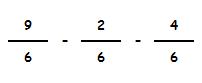
Restamos sus numeradores y mantenemos el denominador:
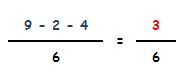
2.- Fracciones con distinto denominador
En este caso para sumar o restar fracciones:
Lo primero que hay que hacer es buscar un denominador común a todas ellas.
Luego sustituir las fracciones originales por fracciones equivalentes con este denominador común.
Y ¿cómo se calcula este denominador común?
Una manera sencilla de calcularlo es multiplicar todos los denominadores; el resultado es el denominador común.
Hay una forma más correcta de calcularlo a través del mínimo común múltiplo. Es una forma más compleja que queda para cursos superiores.
Una vez obtenido el denominador común hay que calcular las fracciones equivalentes. Para cada fracción haremos lo siguiente.
Sustituimos su denominador por el denominador común.
Calculamos su numerador de la siguiente manera: dividimos el denominador común por el denominador original de cada fracción. El resultado obtenido lo multiplicamos por el numerador original, obteniendo el numerador de la fracción equivalente.
Es más fácil ver todo esto con un ejemplo:
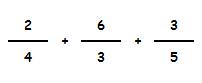
Vamos a calcular las fracciones equivalentes:
Primero calculamos el denominador común: 4 x 3 x 5 = 60
Ahora vamos a calcular el numerador equivalente de cada fracción:
Primera fracción:
Dividimos el denominador común entre su denominador: 60 : 4 =15
Multiplicamos este resultado por su numerador: 15 x 2 = 30
Segunda fracción:
Dividimos el denominador común entre su denominador: 60 : 3 = 20
Multiplicamos este resultado por su numerador: 20 x 6 = 120
Tercera fracción:
Dividimos el denominador común entre su denominador: 60 : 5 =12
Multiplicamos este resultado por su numerador: 12 x 3 = 36
Ya podemos sustituir las fracciones originales por sus fracciones equivalentes:
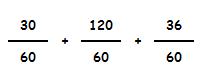
Y procedemos a la suma:
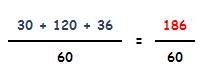
3.- Propiedades:
Las propiedades de la suma de fracciones son las siguientes:
- Propiedad conmutativa
- Propiedad asociativa
- Elemento neutro para la suma
- Elemento opuesto o simétrico
Propiedad conmutativa: La suma de dos fracciones cualesquiera no depende del orden de los sumandos
Esto significa que podemos sumar fracciones en el orden que queramos
Por ejemplo:
1/2 + 3/2 = 4/2
3/2 + 1/2 = 4/2
Entonces: 1/2 + 3/2 = 3/2 + 1/2
Propiedad asociativa: La suma de varias fracciones no dependen del orden en que se asocien
Esto significa que cuando tenemos sumas de varias fracciones, podemos empezar a sumar las fracciones por donde nosotros queramos
Por ejemplo: Para hacer la suma 5/8 + 2/8 + (-3)/8
( 5/8 + 2/8)+ (-3)/8 = 7/8 + (-3)/8 = 4/8
5/8 + ( 2/8 + (-3)/8) = 5/8 + (-1)/8 = 4/8
Entonces: 5/8 + 2/8 + (-3)/8 = ( 5/8 + 2/8)+ (-3)/8 = 5/8 + ( 2/8 + (-3)/8)
Elemento neutro: El elemento neutro para la suma de fracciones es el cero porque si a cualquier fracción le sumamos el cero, obtenemos la misma fracción
Por ejemplo:
3/5 + 0 = 3/5 + 0/5 = (3+0)/5 = 3/5
Elemento opuesto o simétrico: Las fracciones opuestas o simétricas son fracciones que si se suman el resultado es cero
El opuesto de una fracción a/b se puede representar de dos formas: por op(a/b) , o bien por (-a)/b
Opuesto de a/b = op (a/b) = (-a)/b
La suma de una fracción con su opuesta o simétrica da cero
Por ejemplo: Si tenemos la fracción 2/3, su fracción opuesta o simétrica es (-2)/3
Si sumamos las dos fracciones: 2/3 + (-2)/3 = (2-2)/3
Propiedades de los opuestos:
- El opuesto del opuesto de una fracción es la misma fracción
Op (op (2/3)) = 2/3
O también: - ((-2)/3) = 2/3
El opuesto de una suma de fracciones se obtiene cambiando de signo a cada uno de los sumandos
- (a/b + c/d + e/f) = - a/b - c/d - e/f
Por ejemplo: - (1/8 + 5/8 - 2/8) = - 1/8 - 5/8 + 2/8
- Si sumamos una suma de fracciones con su opuesta, el resultado da cero
Si tenemos la suma 1/8 + 5/8 - 2/8
Su opuesta será: - (1/8 + 5/8 - 2/8) = - 1/8 - 5/8 + 2/8
Si sumamos la suma con su opuesta:
1/8 + 5/8 - 2/8 +( - 1/8 - 5/8 + 2/8) = 1/8 + 5/8 - 2/8 - 1/8 - 5/8 + 2/8
Si aplicamos la propiedad asociativa y conmutativa:
1/8 - 1/8 + 5/8 - 5/8 - 2/8 + 2/8 = (1/8 - 1/8) + (5/8 - 5/8) + (- 2/8 + 2/8) = 0 + 0 + 0 = 0
Producto de fracciones: para multiplicar dos o más fracciones, detrás del signo igual trazas una raya y escribes en el numerador el producto de todos los numeradores y como denominador, el producto de todos los denominadores:
Ejemplo:
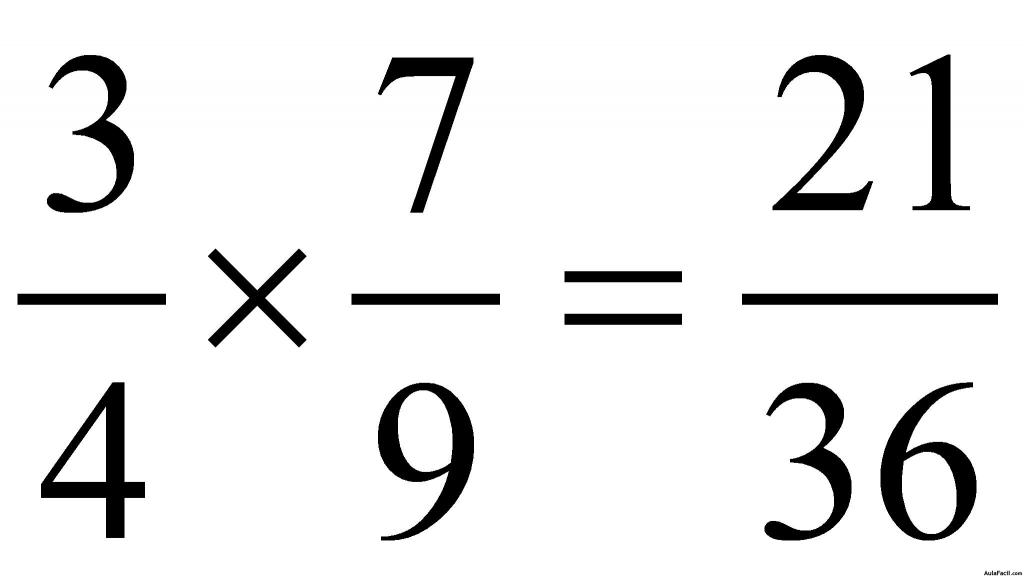 y como 21 y 36 son divisibles por 3, dividimos ambos valores por 3:
y como 21 y 36 son divisibles por 3, dividimos ambos valores por 3: 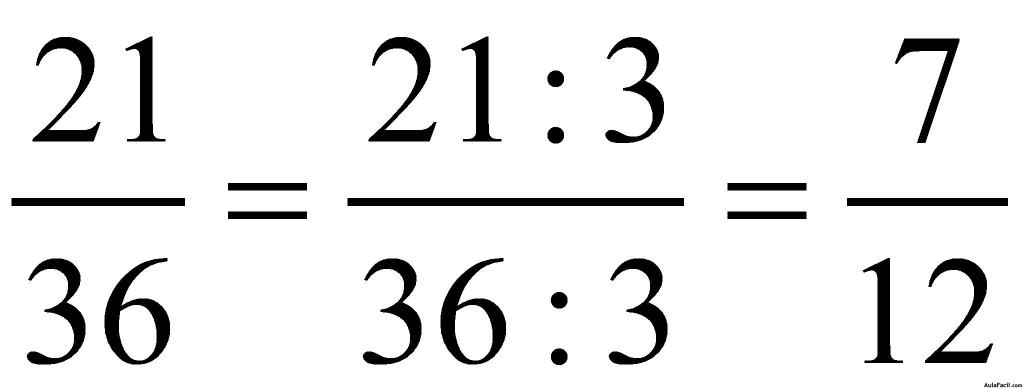
Antes de escribir una fracción como resultado final observa si puedes simplificar, y si se puede no dejes de hacerlo.
Calcula 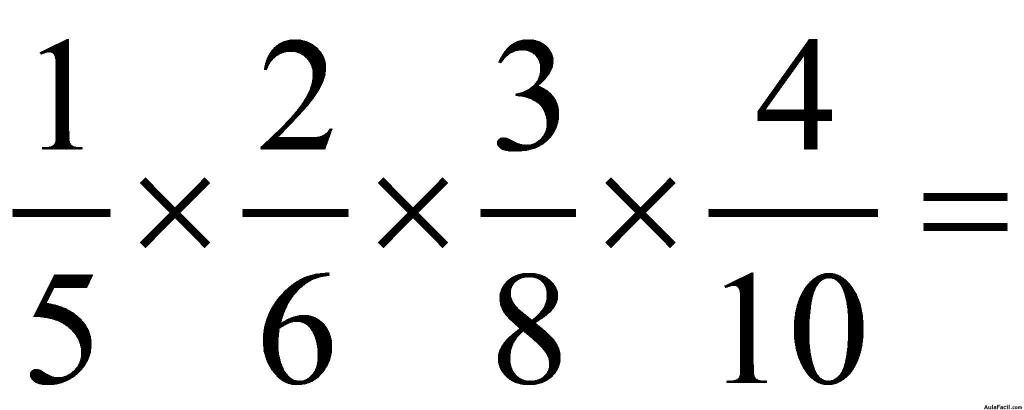
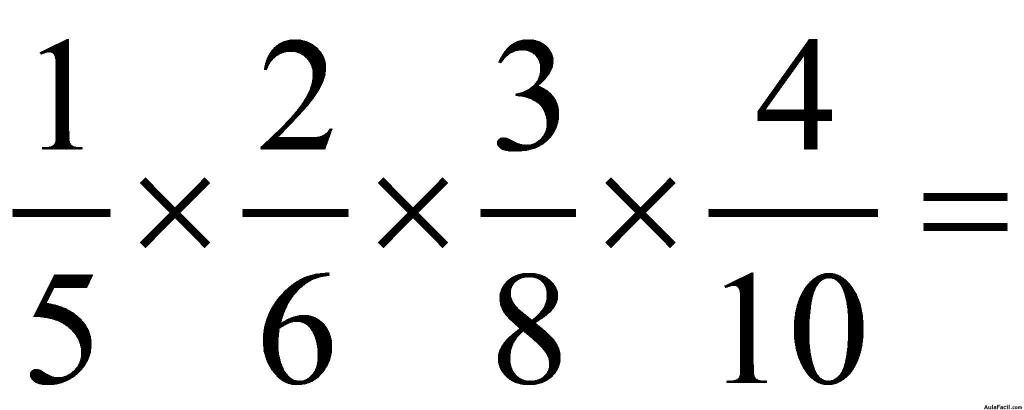
Respuesta simplificada: 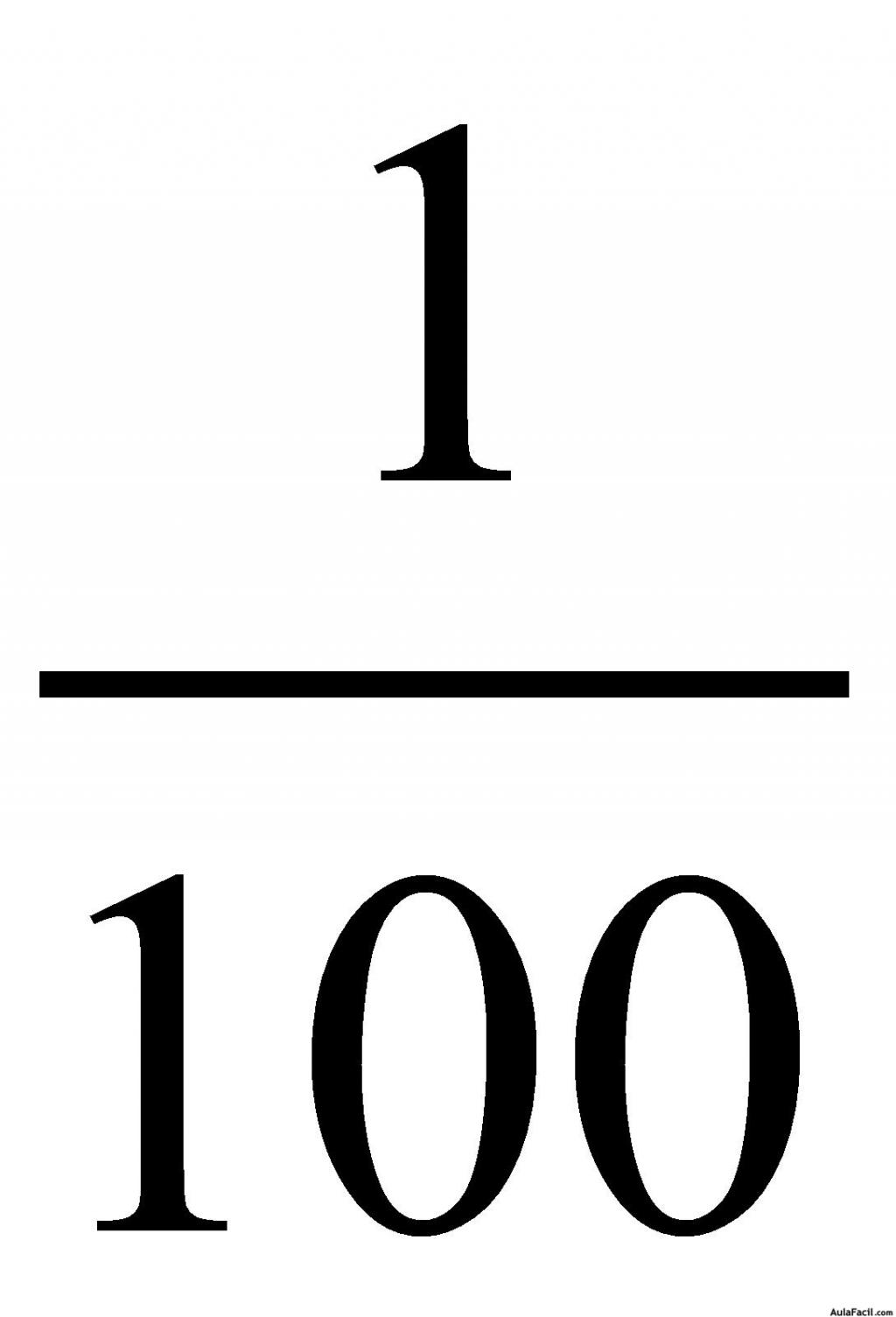
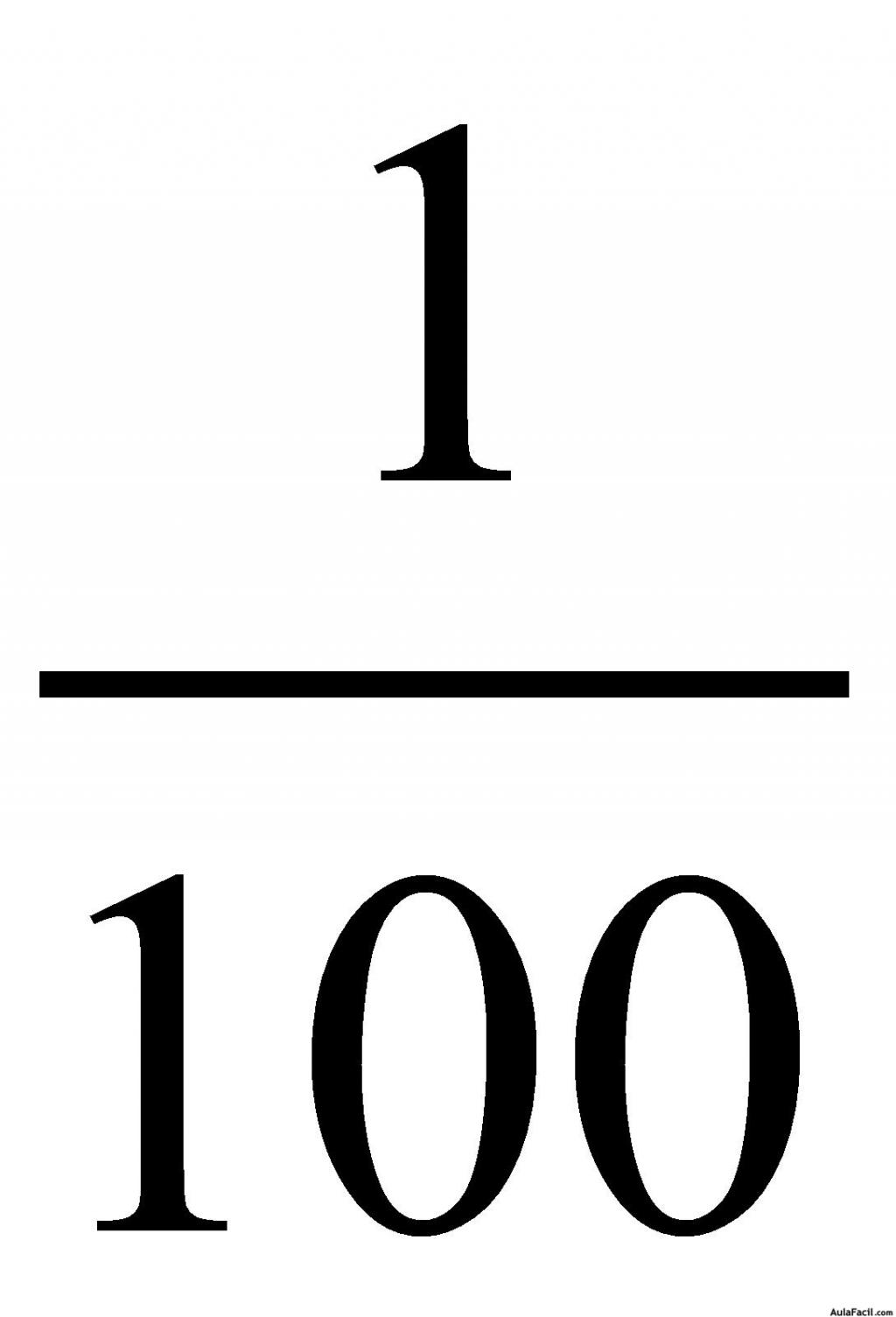
Cociente de fracciones: puedes hacer de dos maneras y te quedas con la que te parezca mejor:
1.- Se multiplican en cruz:
El numerador de la primera fracción por el denominador de la segunda y este resultado figura como numerador resultante. El denominador es el producto del denominador de la primea fracción por el numerador de la segunda. Lo comprenderás mejor si miras el ejemplo:
Ejemplo: 

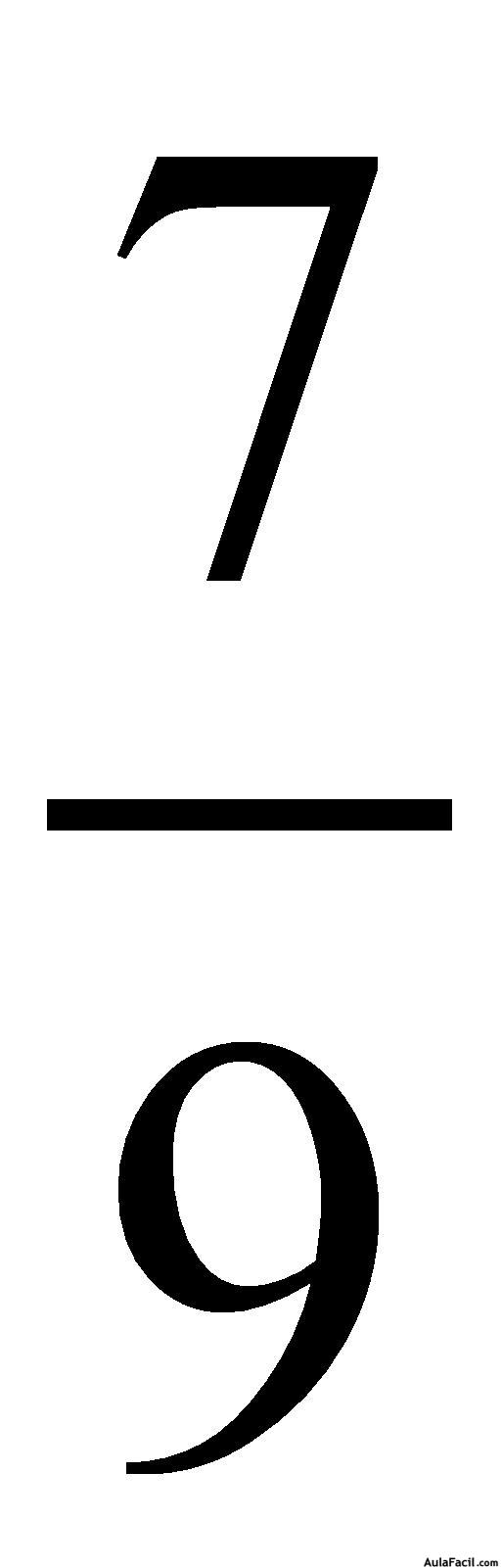


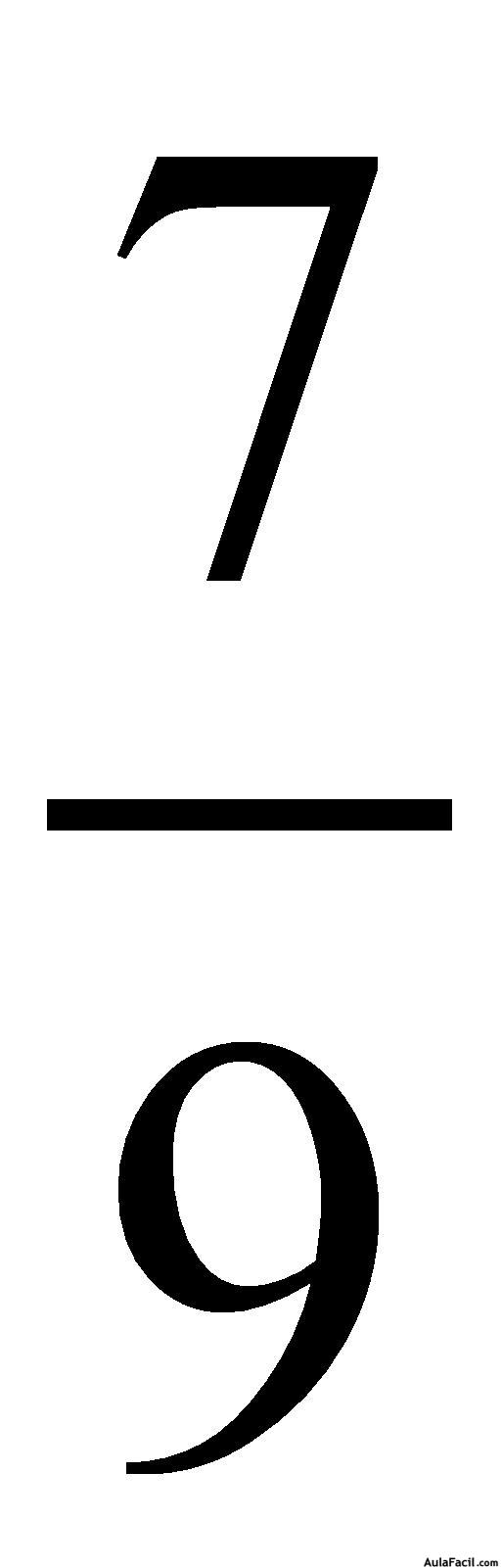
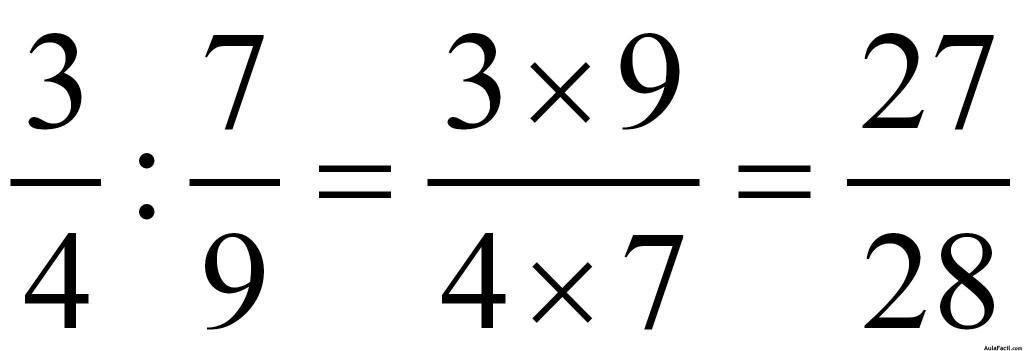
2.- La otra manera de dividir fracciones, todavía es más fácil. A la segunda fracción le inviertes sus términos. Esto quiere decir que donde está el numerador colocas su denominador y donde está el denominador su numerador y después haces lo mismo que para multiplicar fracciones:
Ejemplo:
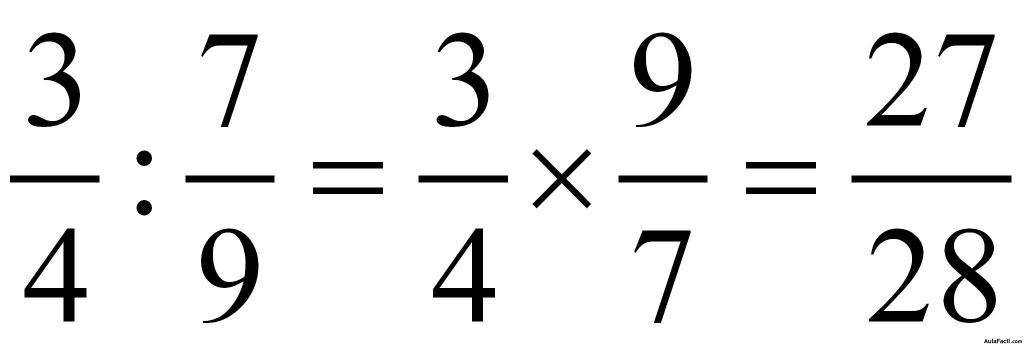
Uso cotidiano:
¿Qué entiende la gente por fracción?Si preguntamos qué es una fracción quizá nos encontremos con respuestas tipo:- Dos números separados por una raya.- Es la parte de un todo
- Por ejemplo: 1/2
Muchos niños se preguntan y nos preguntan para qué se estudian las fracciones y hay que saber dar razones de ello para que crezca su motivación a aprenderlo.
Algunos ejemplos que podemos indicar para ello podrían ser : el reparto de la tarta de un cumpleaños, de una pizza o tableta de chocolate, al ir a la mercado y querer comprar medio kilo de fresas o tres cuartos de carne picada para hamburguesas o si nos queremos hacer una cometa y queremos comprar tela para ella, hacer un pastel siguiendo una receta, etc.
Ejercicio como ejemplo:

- Buñuelos : 4 euros/ kg
- Galletas chocolate: 3 euros/kg
- Galletas mantequilla : 2 euros / kg
- Croissants normal: 3 euros/ kg
- Croissants chocolate : 4 euros / kg
Esta tarde he ido a comprar con mi madre a la pastelería algunos bollos para celebrar el día de la madre. En casa seremos unos cuantos ya que es allí donde nos juntamos para las celebraciones. Vamos a ser como 15 ya que vendrán también mis tíos, primos y abuelos.
- ¿Me da tres cuartos de buñuelos?
- Yo quiero medio de galletas de mantequilla y cuarto y mitad de chocolate
- Póngame medio de croissants de chocolate y la mitad de cuarto de normales.
Cuando nos tocó mi madre compró lo que necesitaba y nos fuimos a casa.
Al llegar, mi madre me pidió que fuera a buscar un papel y un lápiz y que volviera a la cocina. Eso hice y me dijo:
- ¿Puedes contestarme a estas preguntas?
- Cuando estábamos en la pastelería el primer señor pidió tres cuartos de buñuelos, ¿ cuánta es la cantidad en gramos que se ha llevado? ¿ y cuanto le costó?, ¿y al segundo? ¿ y entre todos?
Rápidamente hice la cuenta y también la del resto de los clientes de la pastelería.
Como sabía qué era una fracción pude resolver las preguntas que me hizo mi madre en la cocina.
Ejercicios de repaso:
1. ¿Qué fracción se muestra en cada modelo?
3. Simplificación de fracciones
4. Comparación de fracciones
5. Operaciones de fracciones
A continuación os dejo una sería de juegos que se pueden realizar con los niños una vez hayamos acabado el tema de las fracciones para afianzar conocimientos a través de juegos de mesa.
Es aconsejable hacer grupos para la realización de las actividades,
1. Dominó de fracciones
El juego consiste en ir uniendo cada pieza del dominó siendo necesario que los niñ@s conozcan tanto cómo se escribe la fracción así como la imagen que representa.
2. Parchís de fracciones:
Este juego tiene como objetivo afianzar las operaciones aritméticas con fracciones básicas además de trabajar las matemáticas de una forma lúdica e impulsar las actividades en grupo en clase de matemáticas.
El alumn@ al llegar a una casilla que contiene una operación debe realizarla. Si la operación se hace correctamente nos quedaremos en la casilla pero si el jugador ha fallado en la operación, debe volver a su sitio anterior, perdiendo su turno.
3. Sudoku de fracciones:
El objetivo del juego de Sudoku es completar los casilleros en blanco con los números de tal manera que se cumplan las siguientes condiciones:
- Ninguna columna (vertical) tenga números repetidos
- Ninguna fila (horizontal) tenga números repetidos
- Ningún cuadrado interior 2x2 (marcado con bordes gruesos) tenga números repetidos
La adaptación de este juego para enseñar fracciones en matemáticas consiste en utilizar representaciones gráficas de las fracciones propias en las casillas. Las fracciones son representadas de cuatro maneras diferentes usando: tortas, polígonos, barras, y bloques. Además tienen un código de color.
Los estudiantes deberán llenar los espacios vacíos con los números fraccionarios correspondientes.
Al intentar solucionar los juegos los estudiantes deberán alternar mentalmente entre las representaciones gráficas y simbólicas de las fracciones. El mismo juego de Sudoku da retroalimentación sobre si una fracción está colocada en una celda correcta o no, ya que, de colocarse una fracción en una casilla incorrecta, otras columnas, o filas, o cuadrados no podrán ser completados. Podría una buena opción para una actividad de clase, o para repasar en casa.
4.Recorta y colorea
Consiste en buscar la fracción que corresponde a cada uno de los nombres que aparecen en la cuadrícula vacía. Recortar y pegar cada uno en su sitio y así obtener el dibujo. Cuando acaben pueden colorear el dibujo
5. Águilas y Búhos
Con este juego pretendemos que los alumnos aprendan a observar las posibles propiedades de una fracción. En efecto, mediante preguntas que sólo admitan como respuestas SI o NO, un equipo debe adivinar el valor de la fracción elegida por el otro equipo.
Por ejemplo se podrá preguntar si se trata:– de una fracción propia o impropia (según el nivel se dirá menor o mayor que la unidad)– de una fracción que da lugar a un decimal exacto o un decimal periódico.– de una fracción irreducible. /- de una fracción decimal.– de una fracción mayor que …, menor que … etc.Nivel: 1º-2º de ESOMaterial necesario:– Un tablero para cada dos equipos.- 36 fichas por cada dos equipos.Reglas del juego:– Juego para dos equipos enfrentados de 3, 4, 5 o 6 personas cada uno. Un equipo será los BÚHOS y el otro las ÁGUILAS.– En la primera ronda, empieza el equipo de BÚHOS, eligiendo en secreto una de las fracciones del tablero. Apunta ese valor en un trozo de papel sin que lo vean las ÁGUILAS.
– Las ÁGUILAS tienen el tablero.
– El equipo de las ÁGUILAS tiene que adivinar el valor elegido por los BÚHOS. Para ello tienen que hacer preguntas que solamente admitan como respuesta SI o NO.
Por ejemplo si las ÁGUILAS preguntan si se trata de una fracción propia y los BÚHOS contestan que NO, se debe tapar con una ficha todas las fracciones del tablero que son fracciones propias para rechazarlas. Esto es lo que aparece en la imagen del tablero de la parte superior.
– Si las ÁGUILAS averiguan la fracción con menos de 7 preguntas, ganan un punto.
– En caso contrario han perdido esta ronda.
– En la siguiente ronda se cambian los papeles: las ÁGUILAS escogen una fracción del tablero, la apuntan en secreto y pasan el tablero al equipo de los BÚHOS que tienen que adivinarla.
– Gana el equipo que obtiene más puntuaciones después de varias rondas

















EXCELENTES ESTRATEGIAS Y MATERIALES. PERO TENGO UNA DUDA CON LAS REGLAS DEL JUEGO Y LAS INSTRUCCIONES DEL JUEGO 2: PARCHIS DE FRACCIONES. ME GUSTARÍA NOS EXPLICARAS UN POCO MÁS DE ESO. GRACIAS Y SALUDOS
ResponderEliminar